Question Number 123526 by bramlexs22 last updated on 26/Nov/20
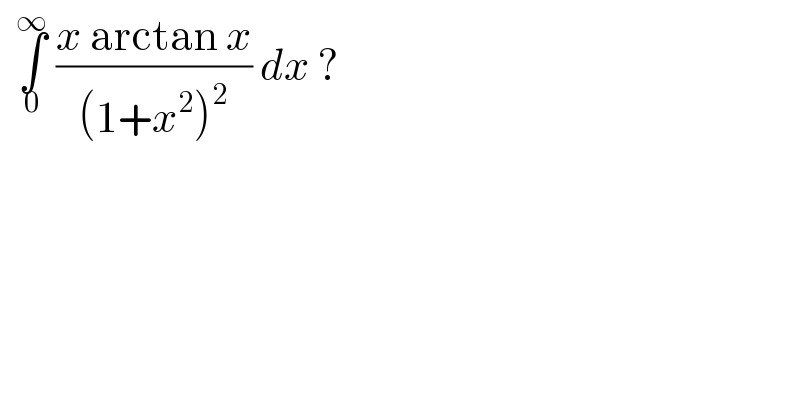
$$\:\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{x}\:\mathrm{arctan}\:{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:? \\ $$
Commented by liberty last updated on 26/Nov/20

$$\frac{\pi}{\mathrm{8}}\:? \\ $$
Commented by bramlexs22 last updated on 26/Nov/20

$${how}\:{sir} \\ $$
Answered by Lordose last updated on 26/Nov/20
![I = ∫_( 0) ^( ∞) ((xtan^(−1) (x))/((1+x^2 )^2 ))dx IBP I = (1/2)∫_0 ^( ∞) (1/((1+x^2 )^2 ))dx − ∣((tan^(−1) (x))/(2(1+x^2 )))∣_0 ^∞ Ostrogradski method I = (1/4)[((x/(1+x^2 ))+tan^(−1) (x))]_0 ^∞ − (1/2)[((tan^(−1) (x))/((1+x^2 )))]_0 ^∞ I = (π/8)](https://www.tinkutara.com/question/Q123536.png)
$$ \\ $$$$\mathrm{I}\:=\:\int_{\:\mathrm{0}} ^{\:\infty} \frac{\mathrm{xtan}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{IBP} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:−\:\mid\frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mid_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{Ostrogradski}\:\mathrm{method} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\left(\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)\right]_{\mathrm{0}} ^{\infty} −\:\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{8}} \\ $$
Commented by bramlexs22 last updated on 26/Nov/20

$${thank}\:{you} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Nov/20
![∫_0 ^(π/2) t sint cost dt t=tan^(−1) x =(1/2)∫_0 ^(π/2) tsin2t dt =−[(t/4)cos2t]^(π/2) +(1/8)[sin2t]_0 ^(π/2) dt =(π/8)](https://www.tinkutara.com/question/Q123538.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {t}\:{sint}\:{cost}\:{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:{t}={tan}^{−\mathrm{1}} {x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {tsin}\mathrm{2}{t}\:{dt}\:=−\left[\frac{{t}}{\mathrm{4}}{cos}\mathrm{2}{t}\right]^{\frac{\pi}{\mathrm{2}}} \:+\frac{\mathrm{1}}{\mathrm{8}}\left[{sin}\mathrm{2}{t}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{dt} \\ $$$$=\frac{\pi}{\mathrm{8}} \\ $$
Commented by bramlexs22 last updated on 26/Nov/20

$${thank}\:{you} \\ $$
Answered by mathmax by abdo last updated on 26/Nov/20
![A =∫_0 ^∞ ((xarctanx)/((1+x^2 )^2 ))dx we integrate by parts u^′ =(x/((1+x^2 )^2 )) and v=srctsnx ⇒A =[−(1/(2(1+x^2 )))arctanx]_0 ^∞ +∫_0 ^∞ (1/(2(1+x^(2)) ))(dx/(1+x^2 )) =(1/2)∫_0 ^∞ (dx/((1+x^2 )^2 )) =_(x=tanθ) (1/2)∫_0 ^(π/2) ((1+tan^2 θ)/((1+tan^2 θ)^2 ))dθ =(1/2)∫_0 ^(π/2) cos^2 θ dθ =(1/4)∫_0 ^(π/2) (1+cos(2θ))dθ =(π/8) +(1/8)[sin(2θ)]_0 ^(π/2) =(π/8)+0 =(π/8) A =(π/8)](https://www.tinkutara.com/question/Q123629.png)
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{xarctanx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:\mathrm{we}\:\mathrm{integrate}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}^{'} \:=\frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{and}\:\mathrm{v}=\mathrm{srctsnx}\:\Rightarrow\mathrm{A}\:=\left[−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{arctanx}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\left.\mathrm{2}\right)} \right.}\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=_{\mathrm{x}=\mathrm{tan}\theta} \:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\mathrm{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\right)\mathrm{d}\theta \\ $$$$=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left[\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{8}}+\mathrm{0}\:=\frac{\pi}{\mathrm{8}} \\ $$$$\mathrm{A}\:=\frac{\pi}{\mathrm{8}} \\ $$
