0-x-e-x-1-dx-

Question Number 52550 by Tawa1 last updated on 09/Jan/19

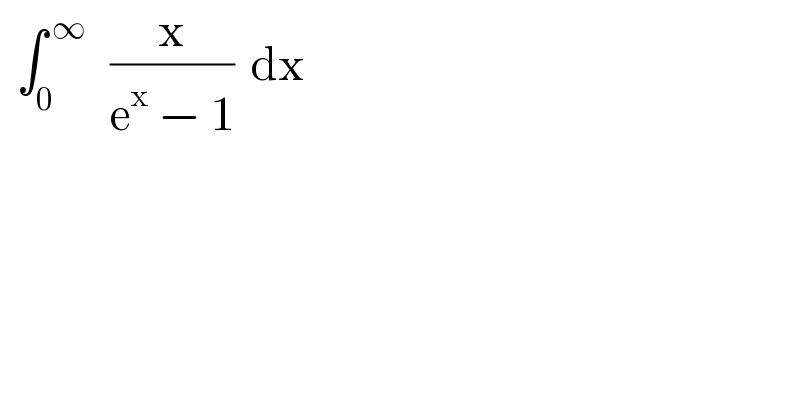
$$\:\:\int_{\mathrm{0}} ^{\:\infty} \:\:\:\frac{\mathrm{x}}{\mathrm{e}^{\mathrm{x}} \:−\:\mathrm{1}}\:\:\mathrm{dx}\: \\ $$

Commented by maxmathsup by imad last updated on 11/Jan/19

let I =∫_0 ^∞ (x/(e^x −1))dx ⇒ I =∫_0 ^∞ ((xe^(−x) )/(1−e^(−x) ))dx =∫_0 ^∞ xe^(−x) (Σ_(n=0) ^∞ e^(−nx) )dx =Σ_(n=0) ^∞ (∫_0 ^∞ x e^(−(n+1)x) dx)=Σ_(n=0) ^∞ A_n A_n =∫_0 ^∞ x e^(−(n+1x) dx =_((n+1)x=t ) ∫_0 ^∞ (t/(n+1)) e^(−t) (dt/(n+1)) =(1/((n+1)^2 ))∫_0 ^∞ t e^(−t) dt but by parts ∫_0 ^∞ t e^(−t) dt =[−t e^(−t) ]_0 ^(+∞) +∫ e^(−t) dt =[−e^(−t) ]_0 ^(+∞) =1 ⇒A_n =(1/((n+1)^2 )) ⇒ I =Σ_(n=0) ^∞ (1/((n+1)^2 )) =Σ_(n=1) ^∞ (1/n^2 ) =(π^2 /6) .

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}}{{e}^{{x}} −\mathrm{1}}{dx}\:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xe}^{−{x}} }{\mathrm{1}−{e}^{−{x}} }{dx}\:=\int_{\mathrm{0}} ^{\infty} \:{xe}^{−{x}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{−{nx}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(\int_{\mathrm{0}} ^{\infty} \:\:{x}\:{e}^{−\left({n}+\mathrm{1}\right){x}} {dx}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} {A}_{{n}} \:\:\: \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:{x}\:{e}^{−\left({n}+\mathrm{1}{x}\right.} {dx}\:=_{\left({n}+\mathrm{1}\right){x}={t}\:} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}}{{n}+\mathrm{1}}\:{e}^{−{t}} \:\:\frac{{dt}}{{n}+\mathrm{1}}\:=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:{t}\:{e}^{−{t}} {dt}\:{but} \\ $$$${by}\:{parts}\:\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} {dt}\:=\left[−{t}\:{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} \:+\int\:{e}^{−{t}} {dt}\:=\left[−{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} =\mathrm{1}\:\Rightarrow{A}_{{n}} =\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:. \\ $$$$ \\ $$

Answered by Smail last updated on 09/Jan/19

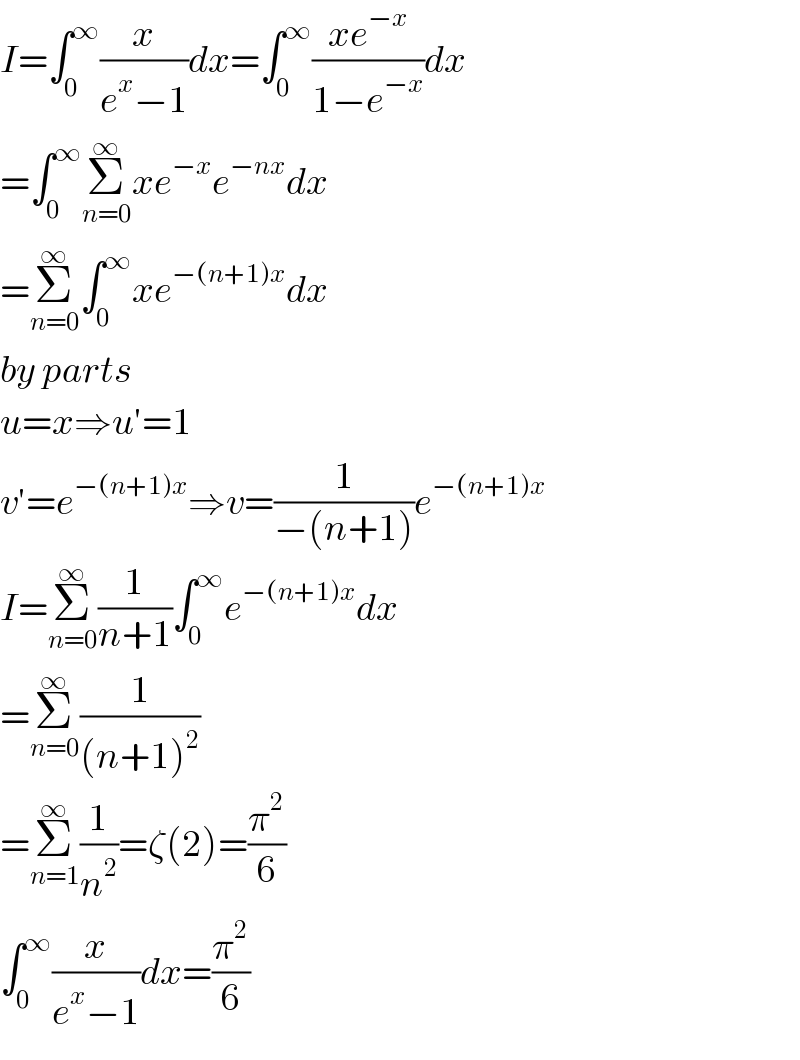
I=∫_0 ^∞ (x/(e^x −1))dx=∫_0 ^∞ ((xe^(−x) )/(1−e^(−x) ))dx =∫_0 ^∞ Σ_(n=0) ^∞ xe^(−x) e^(−nx) dx =Σ_(n=0) ^∞ ∫_0 ^∞ xe^(−(n+1)x) dx by parts u=x⇒u′=1 v′=e^(−(n+1)x) ⇒v=(1/(−(n+1)))e^(−(n+1)x) I=Σ_(n=0) ^∞ (1/(n+1))∫_0 ^∞ e^(−(n+1)x) dx =Σ_(n=0) ^∞ (1/((n+1)^2 )) =Σ_(n=1) ^∞ (1/n^2 )=ζ(2)=(π^2 /6) ∫_0 ^∞ (x/(e^x −1))dx=(π^2 /6)

$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{x}}{{e}^{{x}} −\mathrm{1}}{dx}=\int_{\mathrm{0}} ^{\infty} \frac{{xe}^{−{x}} }{\mathrm{1}−{e}^{−{x}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{xe}^{−{x}} {e}^{−{nx}} {dx} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {xe}^{−\left({n}+\mathrm{1}\right){x}} {dx} \\ $$$${by}\:{parts} \\ $$$${u}={x}\Rightarrow{u}'=\mathrm{1} \\ $$$${v}'={e}^{−\left({n}+\mathrm{1}\right){x}} \Rightarrow{v}=\frac{\mathrm{1}}{−\left({n}+\mathrm{1}\right)}{e}^{−\left({n}+\mathrm{1}\right){x}} \\ $$$${I}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} {e}^{−\left({n}+\mathrm{1}\right){x}} {dx} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}}{{e}^{{x}} −\mathrm{1}}{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Commented by Tawa1 last updated on 09/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply