0-x-e-x-4-dx-

Question Number 126788 by john_santu last updated on 24/Dec/20

$$\:\sigma\:=\:\underset{\mathrm{0}} {\overset{\:\:\:\:\:\infty} {\int}}\sqrt{{x}}\:{e}^{−{x}/\mathrm{4}} \:{dx}\:=\:?\: \\ $$

Answered by Ar Brandon last updated on 24/Dec/20

x=u^2 ⇒ dx=2udu σ=2∫_0 ^∞ u^2 e^(−u^2 /4) du e^(−u^2 /4) =t ⇒ −(1/2)ue^(−u^2 /4) du=dt σ=−4∫_0 ^∞ u∙(−(1/2)ue^(−u^2 /4) )du =−4{ue^(−u^2 /4) −∫e^(−u^2 /4) du}_0 ^∞ =4∫_0 ^∞ e^(−u^2 /4) du { ((I=∫_0 ^∞ e^(−x^2 /4) dx)),((I=∫_0 ^∞ e^(−y^2 /4) dy)) :} I^2 =∫_0 ^∞ ∫_0 ^∞ e^(−(x^2 +y^2 )/4) dxdy =∫_0 ^(π/2) ∫_0 ^∞ re^(−r^2 /4) drdθ=−2∫_0 ^(π/2) ∫_0 ^∞ −(1/2)re^(−r^2 /4) drdθ =−2[(θ/1)]_0 ^(π/2) [e^(−r^2 /4) ]_0 ^∞ =−((2/1))((π/2))(0−1)=π I=(√π) σ=4I=4(√π)

$$\mathrm{x}=\mathrm{u}^{\mathrm{2}} \:\Rightarrow\:\mathrm{dx}=\mathrm{2udu} \\ $$$$\sigma=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \mathrm{u}^{\mathrm{2}} \mathrm{e}^{−\mathrm{u}^{\mathrm{2}} /\mathrm{4}} \mathrm{du} \\ $$$$\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} /\mathrm{4}} =\mathrm{t}\:\Rightarrow\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ue}^{−\mathrm{u}^{\mathrm{2}} /\mathrm{4}} \mathrm{du}=\mathrm{dt} \\ $$$$\sigma=−\mathrm{4}\int_{\mathrm{0}} ^{\infty} \mathrm{u}\centerdot\left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ue}^{−\mathrm{u}^{\mathrm{2}} /\mathrm{4}} \right)\mathrm{du} \\ $$$$\:\:\:=−\mathrm{4}\left\{\mathrm{ue}^{−\mathrm{u}^{\mathrm{2}} /\mathrm{4}} −\int\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} /\mathrm{4}} \mathrm{du}\right\}_{\mathrm{0}} ^{\infty} \\ $$$$\:\:\:=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{u}^{\mathrm{2}} /\mathrm{4}} \mathrm{du} \\ $$$$\begin{cases}{\mathcal{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} /\mathrm{4}} \mathrm{dx}}\\{\mathcal{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{y}^{\mathrm{2}} /\mathrm{4}} \mathrm{dy}}\end{cases}\: \\ $$$$\mathcal{I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)/\mathrm{4}} \mathrm{dxdy} \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\infty} \mathrm{re}^{−\mathrm{r}^{\mathrm{2}} /\mathrm{4}} \mathrm{drd}\theta=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{re}^{−\mathrm{r}^{\mathrm{2}} /\mathrm{4}} \mathrm{drd}\theta \\ $$$$\:\:\:\:\:=−\mathrm{2}\left[\frac{\theta}{\mathrm{1}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left[\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} /\mathrm{4}} \right]_{\mathrm{0}} ^{\infty} =−\left(\frac{\mathrm{2}}{\mathrm{1}}\right)\left(\frac{\pi}{\mathrm{2}}\right)\left(\mathrm{0}−\mathrm{1}\right)=\pi \\ $$$$\mathcal{I}=\sqrt{\pi} \\ $$$$\sigma=\mathrm{4}\mathcal{I}=\mathrm{4}\sqrt{\pi} \\ $$

Answered by john_santu last updated on 24/Dec/20

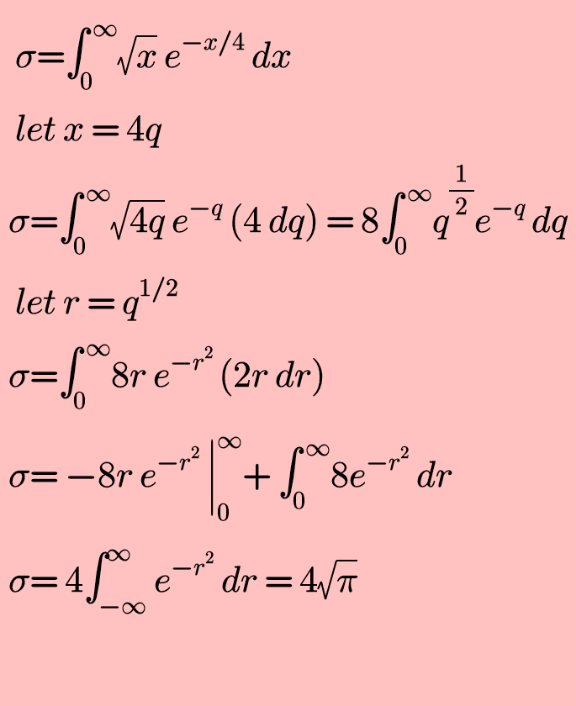
Answered by Dwaipayan Shikari last updated on 24/Dec/20

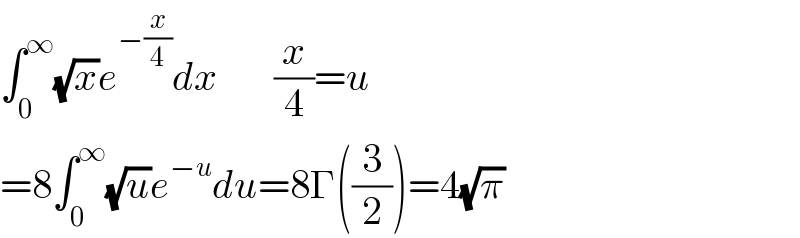
∫_0 ^∞ (√x)e^(−(x/4)) dx (x/4)=u =8∫_0 ^∞ (√u)e^(−u) du=8Γ((3/2))=4(√π)

$$\int_{\mathrm{0}} ^{\infty} \sqrt{{x}}{e}^{−\frac{{x}}{\mathrm{4}}} {dx}\:\:\:\:\:\:\:\frac{{x}}{\mathrm{4}}={u} \\ $$$$=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \sqrt{{u}}{e}^{−{u}} {du}=\mathrm{8}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\mathrm{4}\sqrt{\pi} \\ $$

Answered by mathmax by abdo last updated on 24/Dec/20

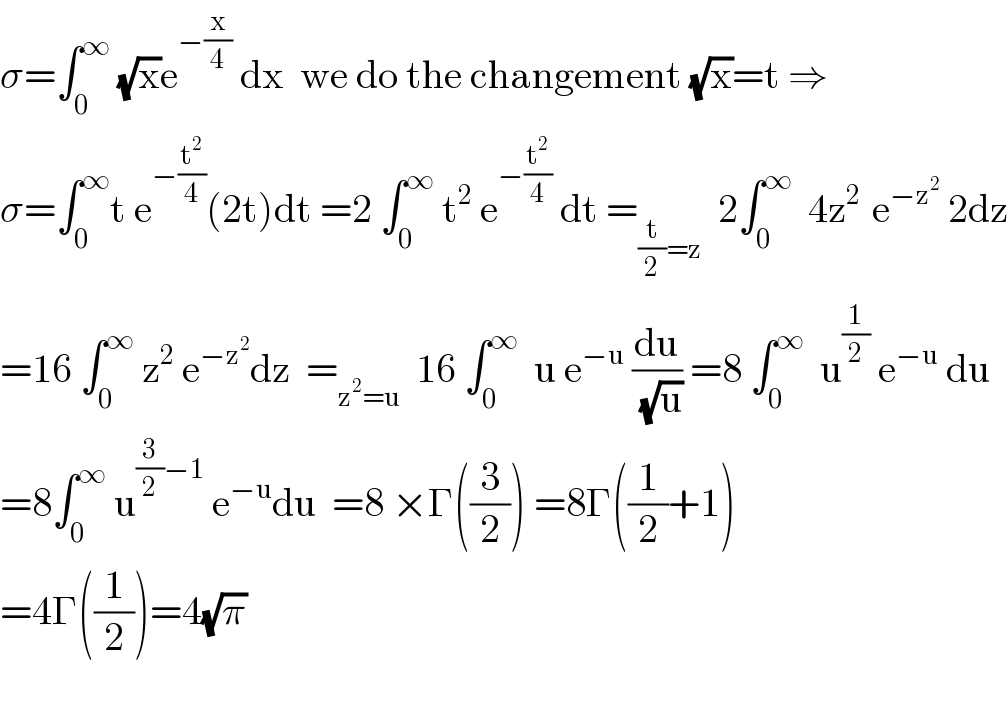
σ=∫_0 ^∞ (√x)e^(−(x/4)) dx we do the changement (√x)=t ⇒ σ=∫_0 ^∞ t e^(−(t^2 /4)) (2t)dt =2 ∫_0 ^∞ t^2 e^(−(t^2 /4)) dt =_((t/2)=z) 2∫_0 ^∞ 4z^(2 ) e^(−z^2 ) 2dz =16 ∫_0 ^∞ z^2 e^(−z^2 ) dz =_(z^2 =u) 16 ∫_0 ^∞ u e^(−u) (du/( (√u))) =8 ∫_0 ^∞ u^(1/2) e^(−u) du =8∫_0 ^∞ u^((3/2)−1) e^(−u) du =8 ×Γ((3/2)) =8Γ((1/2)+1) =4Γ((1/2))=4(√π)

$$\sigma=\int_{\mathrm{0}} ^{\infty} \:\sqrt{\mathrm{x}}\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{4}}} \:\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\mathrm{x}}=\mathrm{t}\:\Rightarrow \\ $$$$\sigma=\int_{\mathrm{0}} ^{\infty} \mathrm{t}\:\mathrm{e}^{−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}}} \left(\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}}} \:\mathrm{dt}\:=_{\frac{\mathrm{t}}{\mathrm{2}}=\mathrm{z}} \:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{4z}^{\mathrm{2}\:} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \:\mathrm{2dz} \\ $$$$=\mathrm{16}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\:\:=_{\mathrm{z}^{\mathrm{2}} =\mathrm{u}} \:\:\mathrm{16}\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{u}\:\mathrm{e}^{−\mathrm{u}} \:\frac{\mathrm{du}}{\:\sqrt{\mathrm{u}}}\:=\mathrm{8}\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{u}} \:\mathrm{du} \\ $$$$=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{u}} \mathrm{du}\:\:=\mathrm{8}\:×\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\mathrm{8}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right) \\ $$$$=\mathrm{4}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{4}\sqrt{\pi} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply