Question Number 109208 by Dwaipayan Shikari last updated on 21/Aug/20
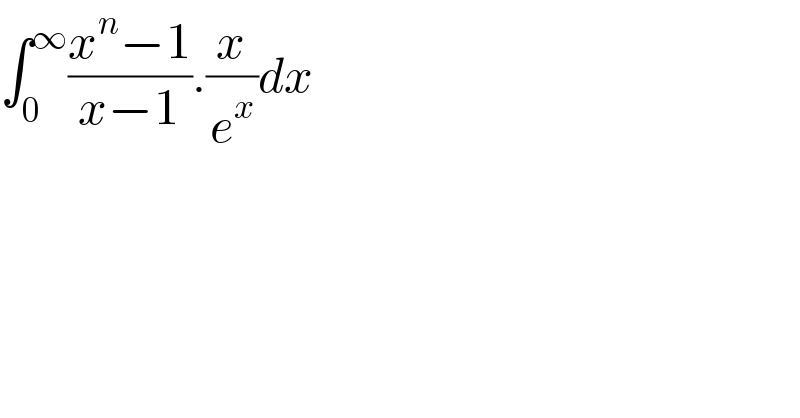
$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{n}} −\mathrm{1}}{{x}−\mathrm{1}}.\frac{{x}}{{e}^{{x}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 22/Aug/20
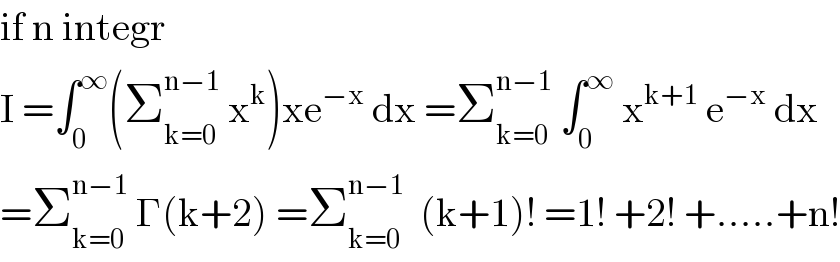
$$\mathrm{if}\:\mathrm{n}\:\mathrm{integr}\: \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\mathrm{x}^{\mathrm{k}} \right)\mathrm{xe}^{−\mathrm{x}} \:\mathrm{dx}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{k}+\mathrm{1}} \:\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\Gamma\left(\mathrm{k}+\mathrm{2}\right)\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\:\left(\mathrm{k}+\mathrm{1}\right)!\:=\mathrm{1}!\:+\mathrm{2}!\:+…..+\mathrm{n}! \\ $$
Commented by Dwaipayan Shikari last updated on 22/Aug/20
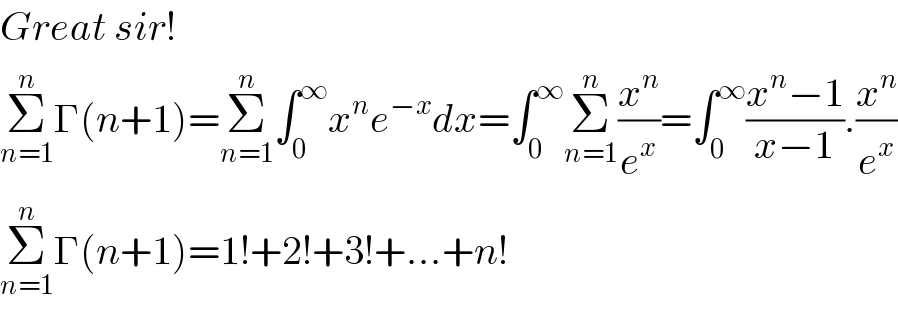
$${Great}\:{sir}! \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\Gamma\left({n}+\mathrm{1}\right)=\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\int_{\mathrm{0}} ^{\infty} {x}^{{n}} {e}^{−{x}} {dx}=\int_{\mathrm{0}} ^{\infty} \underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{x}^{{n}} }{{e}^{{x}} }=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{n}} −\mathrm{1}}{{x}−\mathrm{1}}.\frac{{x}^{{n}} }{{e}^{{x}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\Gamma\left({n}+\mathrm{1}\right)=\mathrm{1}!+\mathrm{2}!+\mathrm{3}!+…+{n}! \\ $$
