Question Number 144926 by ArielVyny last updated on 30/Jun/21
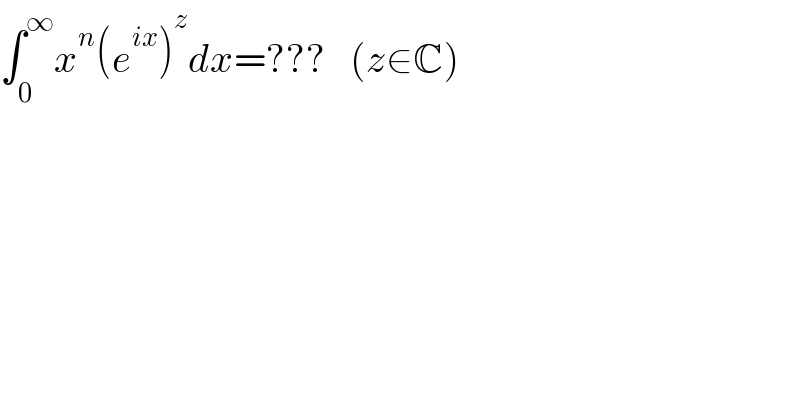
$$\int_{\mathrm{0}} ^{\infty} {x}^{{n}} \left({e}^{{ix}} \right)^{{z}} {dx}=???\:\:\:\left({z}\in\mathbb{C}\right) \\ $$
Answered by mathmax by abdo last updated on 30/Jun/21
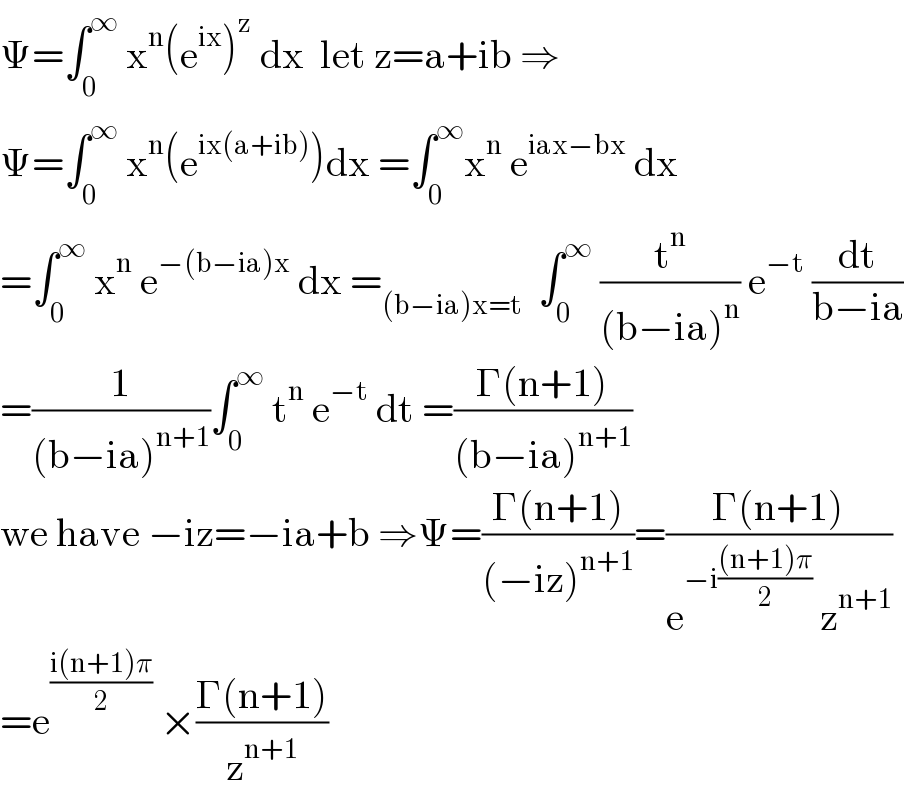
$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{z}} \:\mathrm{dx}\:\:\mathrm{let}\:\mathrm{z}=\mathrm{a}+\mathrm{ib}\:\Rightarrow \\ $$$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \left(\mathrm{e}^{\mathrm{ix}\left(\mathrm{a}+\mathrm{ib}\right)} \right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{n}} \:\mathrm{e}^{\mathrm{iax}−\mathrm{bx}} \:\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{e}^{−\left(\mathrm{b}−\mathrm{ia}\right)\mathrm{x}} \:\mathrm{dx}\:=_{\left(\mathrm{b}−\mathrm{ia}\right)\mathrm{x}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{n}} }{\left(\mathrm{b}−\mathrm{ia}\right)^{\mathrm{n}} }\:\mathrm{e}^{−\mathrm{t}} \:\frac{\mathrm{dt}}{\mathrm{b}−\mathrm{ia}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{b}−\mathrm{ia}\right)^{\mathrm{n}+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:=\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\left(\mathrm{b}−\mathrm{ia}\right)^{\mathrm{n}+\mathrm{1}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:−\mathrm{iz}=−\mathrm{ia}+\mathrm{b}\:\Rightarrow\Psi=\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\left(−\mathrm{iz}\right)^{\mathrm{n}+\mathrm{1}} }=\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{e}^{−\mathrm{i}\frac{\left(\mathrm{n}+\mathrm{1}\right)\pi}{\mathrm{2}}} \:\mathrm{z}^{\mathrm{n}+\mathrm{1}} } \\ $$$$=\mathrm{e}^{\frac{\mathrm{i}\left(\mathrm{n}+\mathrm{1}\right)\pi}{\mathrm{2}}} \:×\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{z}^{\mathrm{n}+\mathrm{1}} } \\ $$
