Question Number 145408 by Dwaipayan Shikari last updated on 04/Jul/21
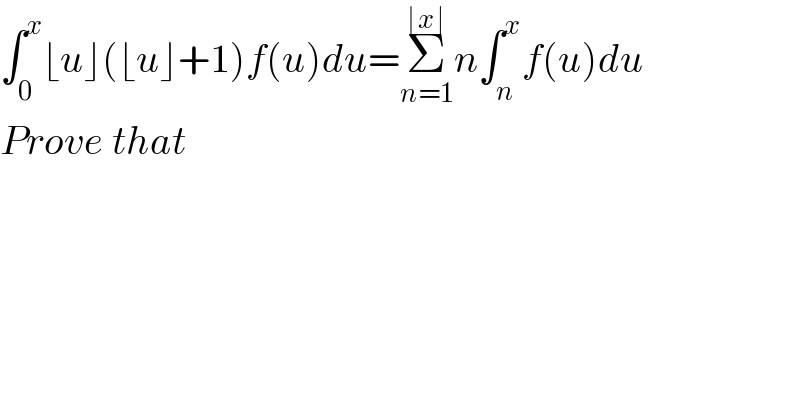
$$\int_{\mathrm{0}} ^{{x}} \lfloor{u}\rfloor\left(\lfloor{u}\rfloor+\mathrm{1}\right){f}\left({u}\right){du}=\underset{{n}=\mathrm{1}} {\overset{\lfloor{x}\rfloor} {\sum}}{n}\int_{{n}} ^{{x}} {f}\left({u}\right){du}\:\: \\ $$$${Prove}\:{that} \\ $$
