Question Number 146621 by 777316 last updated on 14/Jul/21
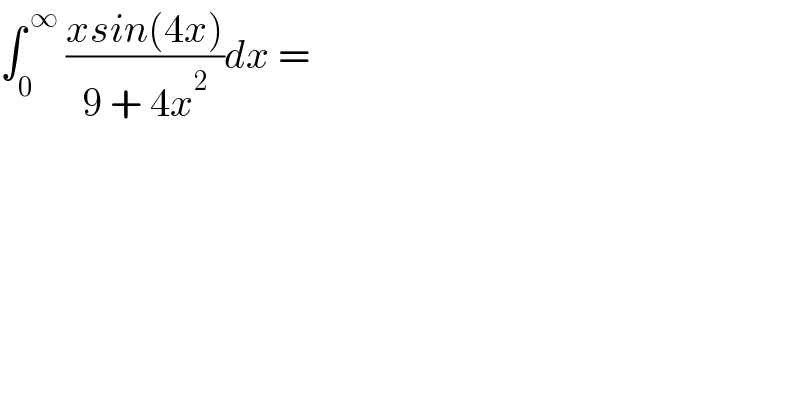
$$\int_{\mathrm{0}} ^{\:\infty} \:\frac{{xsin}\left(\mathrm{4}{x}\right)}{\mathrm{9}\:+\:\mathrm{4}{x}^{\mathrm{2}} }{dx}\:=\: \\ $$
Answered by mathmax by abdo last updated on 14/Jul/21
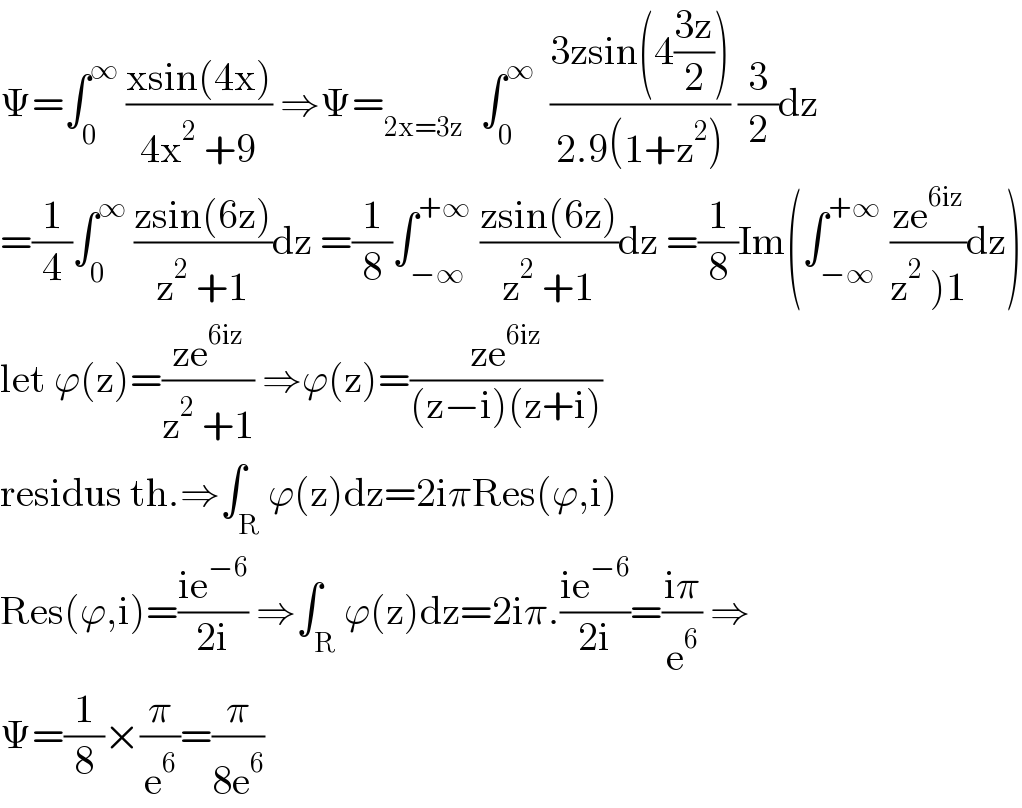
$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{xsin}\left(\mathrm{4x}\right)}{\mathrm{4x}^{\mathrm{2}} \:+\mathrm{9}}\:\Rightarrow\Psi=_{\mathrm{2x}=\mathrm{3z}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{3zsin}\left(\mathrm{4}\frac{\mathrm{3z}}{\mathrm{2}}\right)}{\mathrm{2}.\mathrm{9}\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)}\:\frac{\mathrm{3}}{\mathrm{2}}\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{zsin}\left(\mathrm{6z}\right)}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dz}\:=\frac{\mathrm{1}}{\mathrm{8}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{zsin}\left(\mathrm{6z}\right)}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dz}\:=\frac{\mathrm{1}}{\mathrm{8}}\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{ze}^{\mathrm{6iz}} }{\left.\mathrm{z}^{\mathrm{2}} \:\right)\mathrm{1}}\mathrm{dz}\right) \\ $$$$\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{ze}^{\mathrm{6iz}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{ze}^{\mathrm{6iz}} }{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)} \\ $$$$\mathrm{residus}\:\mathrm{th}.\Rightarrow\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\mathrm{Res}\left(\varphi,\mathrm{i}\right) \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)=\frac{\mathrm{ie}^{−\mathrm{6}} }{\mathrm{2i}}\:\Rightarrow\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi.\frac{\mathrm{ie}^{−\mathrm{6}} }{\mathrm{2i}}=\frac{\mathrm{i}\pi}{\mathrm{e}^{\mathrm{6}} }\:\Rightarrow \\ $$$$\Psi=\frac{\mathrm{1}}{\mathrm{8}}×\frac{\pi}{\mathrm{e}^{\mathrm{6}} }=\frac{\pi}{\mathrm{8e}^{\mathrm{6}} } \\ $$
Answered by KINMATICS last updated on 14/Jul/21
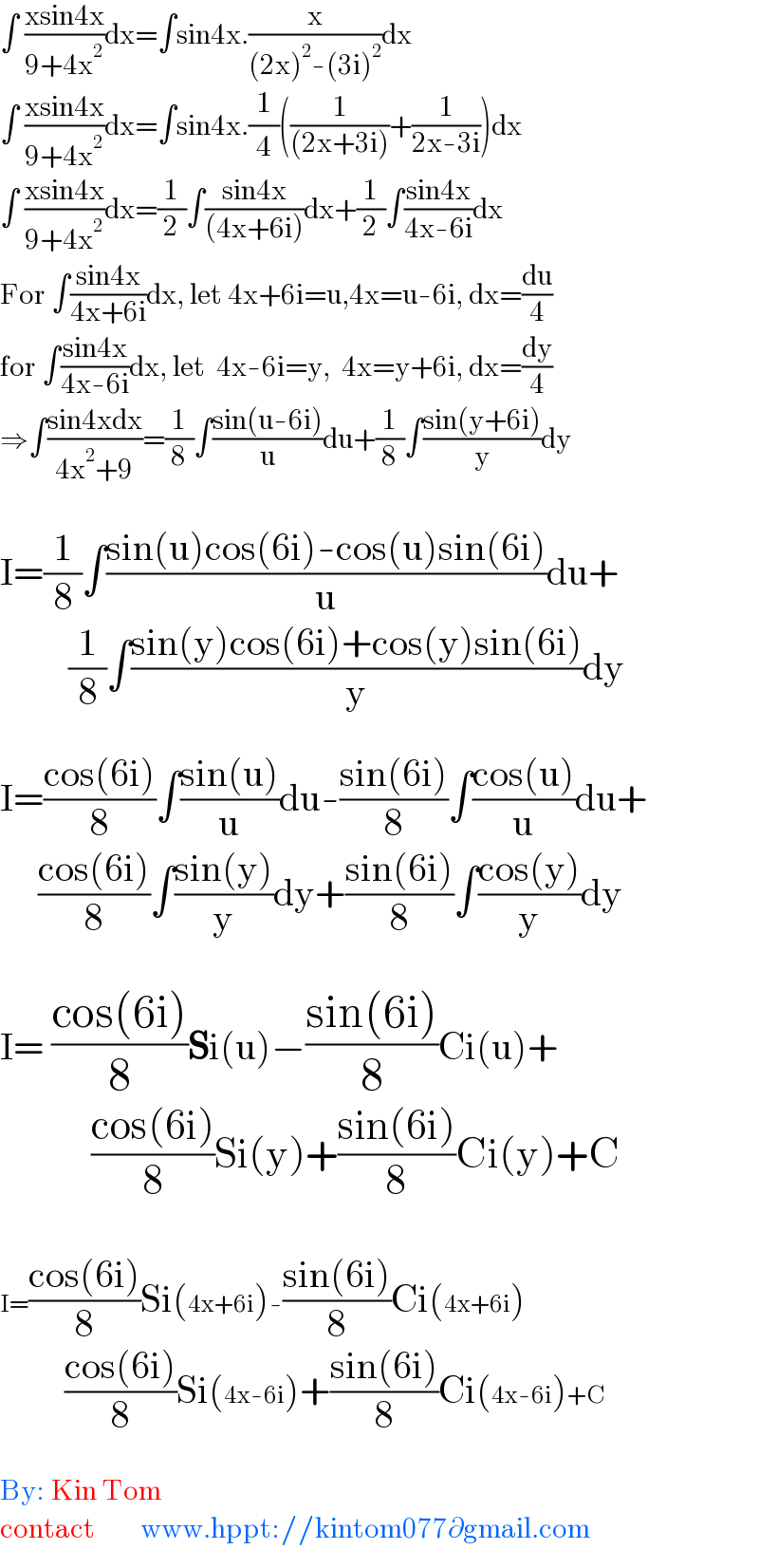
$$\int\:\frac{\mathrm{xsin4x}}{\mathrm{9}+\mathrm{4x}^{\mathrm{2}} }\mathrm{dx}=\int\mathrm{sin4x}.\frac{\mathrm{x}}{\left(\mathrm{2x}\right)^{\mathrm{2}} -\left(\mathrm{3i}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\int\:\frac{\mathrm{xsin4x}}{\mathrm{9}+\mathrm{4x}^{\mathrm{2}} }\mathrm{dx}=\int\mathrm{sin4x}.\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\left(\mathrm{2x}+\mathrm{3i}\right)}+\frac{\mathrm{1}}{\mathrm{2x}-\mathrm{3i}}\right)\mathrm{dx} \\ $$$$\int\:\frac{\mathrm{xsin4x}}{\mathrm{9}+\mathrm{4x}^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{sin4x}}{\left(\mathrm{4x}+\mathrm{6i}\right)}\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{sin4x}}{\mathrm{4x}-\mathrm{6i}}\mathrm{dx} \\ $$$$\mathrm{For}\:\int\frac{\mathrm{sin4x}}{\mathrm{4x}+\mathrm{6i}}\mathrm{dx},\:\mathrm{let}\:\mathrm{4x}+\mathrm{6i}=\mathrm{u},\mathrm{4x}=\mathrm{u}-\mathrm{6i},\:\mathrm{dx}=\frac{\mathrm{du}}{\mathrm{4}} \\ $$$$\mathrm{for}\:\int\frac{\mathrm{sin4x}}{\mathrm{4x}-\mathrm{6i}}\mathrm{dx},\:\mathrm{let}\:\:\mathrm{4x}-\mathrm{6i}=\mathrm{y},\:\:\mathrm{4x}=\mathrm{y}+\mathrm{6i},\:\mathrm{dx}=\frac{\mathrm{dy}}{\mathrm{4}} \\ $$$$\Rightarrow\int\frac{\mathrm{sin4xdx}}{\mathrm{4x}^{\mathrm{2}} +\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{sin}\left(\mathrm{u}-\mathrm{6i}\right)}{\mathrm{u}}\mathrm{du}+\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{sin}\left(\mathrm{y}+\mathrm{6i}\right)}{\mathrm{y}}\mathrm{dy} \\ $$$$ \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{sin}\left(\mathrm{u}\right)\mathrm{cos}\left(\mathrm{6i}\right)-\mathrm{cos}\left(\mathrm{u}\right)\mathrm{sin}\left(\mathrm{6i}\right)}{\mathrm{u}}\mathrm{du}+ \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{sin}\left(\mathrm{y}\right)\mathrm{cos}\left(\mathrm{6i}\right)+\mathrm{cos}\left(\mathrm{y}\right)\mathrm{sin}\left(\mathrm{6i}\right)}{\mathrm{y}}\mathrm{dy} \\ $$$$ \\ $$$$\mathrm{I}=\frac{\mathrm{cos}\left(\mathrm{6i}\right)}{\mathrm{8}}\int\frac{\mathrm{sin}\left(\mathrm{u}\right)}{\mathrm{u}}\mathrm{du}-\frac{\mathrm{sin}\left(\mathrm{6i}\right)}{\mathrm{8}}\int\frac{\mathrm{cos}\left(\mathrm{u}\right)}{\mathrm{u}}\mathrm{du}+ \\ $$$$\:\:\:\:\:\frac{\mathrm{cos}\left(\mathrm{6i}\right)}{\mathrm{8}}\int\frac{\mathrm{sin}\left(\mathrm{y}\right)}{\mathrm{y}}\mathrm{dy}+\frac{\mathrm{sin}\left(\mathrm{6i}\right)}{\mathrm{8}}\int\frac{\mathrm{cos}\left(\mathrm{y}\right)}{\mathrm{y}}\mathrm{dy} \\ $$$$\: \\ $$$$\mathrm{I}=\:\frac{\mathrm{cos}\left(\mathrm{6i}\right)}{\mathrm{8}}\boldsymbol{\mathrm{S}}\mathrm{i}\left(\mathrm{u}\right)−\frac{\mathrm{sin}\left(\mathrm{6i}\right)}{\mathrm{8}}\mathrm{Ci}\left(\mathrm{u}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{cos}\left(\mathrm{6i}\right)}{\mathrm{8}}\mathrm{Si}\left(\mathrm{y}\right)+\frac{\mathrm{sin}\left(\mathrm{6i}\right)}{\mathrm{8}}\mathrm{Ci}\left(\mathrm{y}\right)+\mathrm{C} \\ $$$$\: \\ $$$$\mathrm{I}=\frac{\mathrm{cos}\left(\mathrm{6i}\right)}{\mathrm{8}}\mathrm{Si}\left(\mathrm{4x}+\mathrm{6i}\right)-\frac{\mathrm{sin}\left(\mathrm{6i}\right)}{\mathrm{8}}\mathrm{Ci}\left(\mathrm{4x}+\mathrm{6i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{cos}\left(\mathrm{6i}\right)}{\mathrm{8}}\mathrm{Si}\left(\mathrm{4x}-\mathrm{6i}\right)+\frac{\mathrm{sin}\left(\mathrm{6i}\right)}{\mathrm{8}}\mathrm{Ci}\left(\mathrm{4x}-\mathrm{6i}\right)+\mathrm{C} \\ $$$$ \\ $$$$\mathrm{By}:\:\mathrm{Kin}\:\mathrm{Tom} \\ $$$$\mathrm{contact}\:\:\:\:\:\:\:\:\mathrm{www}.\mathrm{hppt}://\mathrm{kintom077}\partial\mathrm{gmail}.\mathrm{com} \\ $$
