Question Number 173975 by savitar last updated on 22/Jul/22
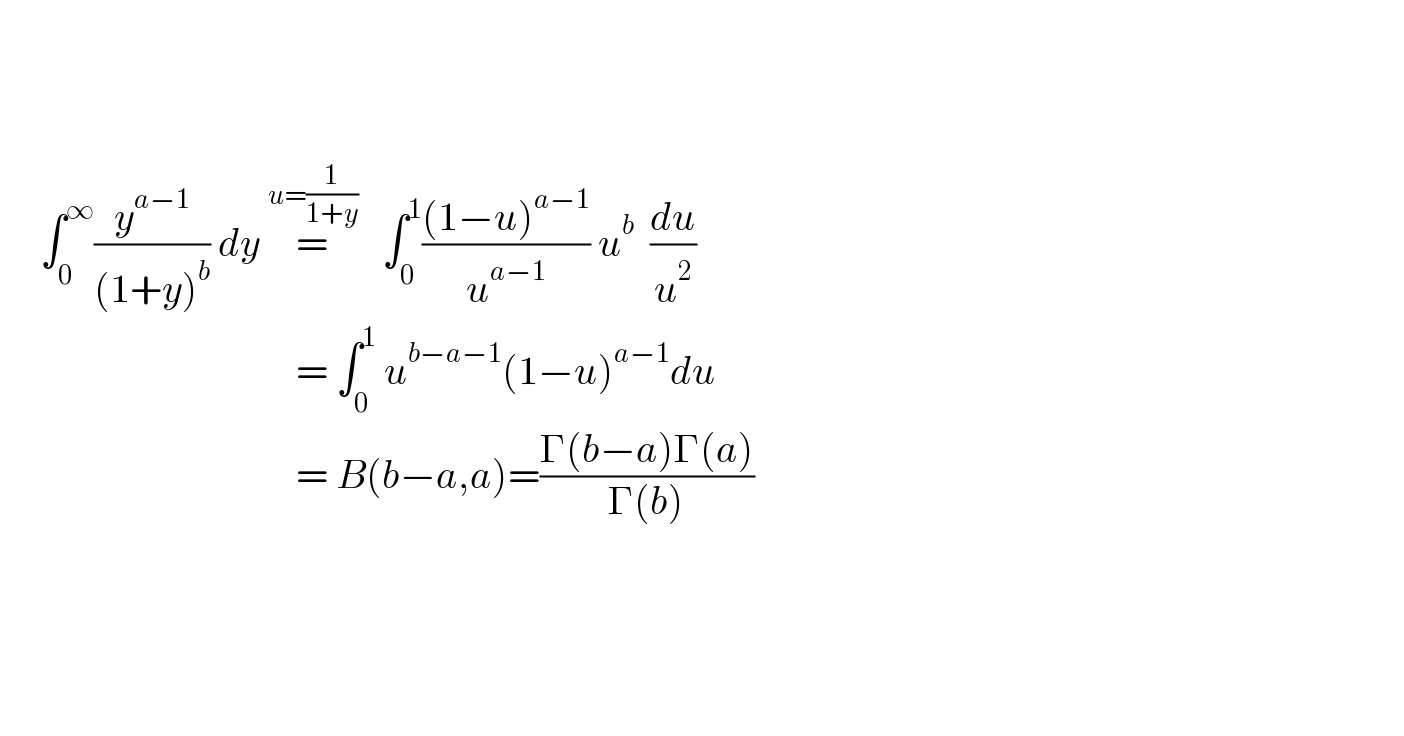
$$ \\ $$$$\: \\ $$$$ \\ $$$$\:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \frac{{y}^{{a}−\mathrm{1}} }{\left(\mathrm{1}+{y}\right)^{{b}} }\:{dy}\:\overset{{u}=\frac{\mathrm{1}}{\mathrm{1}+{y}}} {=}\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{u}\right)^{{a}−\mathrm{1}} }{{u}^{{a}−\mathrm{1}} }\:{u}^{{b}} \:\:\frac{{du}}{{u}^{\mathrm{2}} }\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{u}^{{b}−{a}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{a}−\mathrm{1}} {du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{B}\left({b}−{a},{a}\right)=\frac{\Gamma\left({b}−{a}\right)\Gamma\left({a}\right)}{\Gamma\left({b}\right)} \\ $$$$\:\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
