Menu Close

1-0-1-dx-2x-4-2x-2-1-2-0-x-1-4-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 185836 by greougoury555 last updated on 28/Jan/23
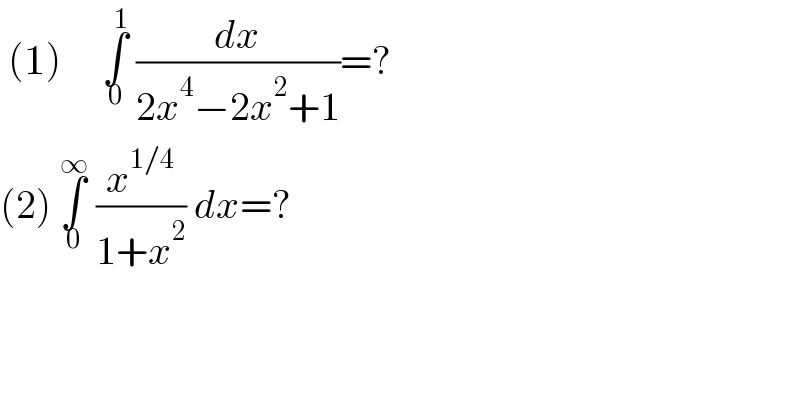
(1) ∫_0 ^1 (dx/(2x^4 −2x^2 +1))=? (2) ∫_0 ^∞ (x^(1/4) /(1+x^2 )) dx=?
$$\:\left(\mathrm{1}\right)\:\:\:\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{dx}}{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}=? \\ $$$$\left(\mathrm{2}\right)\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{x}^{\mathrm{1}/\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}=? \\ $$
Answered by Ar Brandon last updated on 28/Jan/23
I=∫_0 ^1 (dx/(2x^4 −2x^2 +1))=(1/2)∫_0 ^1 ((((√2)x^2 +1)−((√2)x^2 −1))/(2x^4 −2x^2 +1))dx =(1/2)∫_0 ^1 (((√2)x^2 +1)/(2x^4 −2x^2 +1))dx−(1/2)∫_0 ^1 (((√2)x^2 −1)/(2x^4 −2x^2 +1))dx =(1/2)∫_0 ^1 (((√2)+(1/x^2 ))/(2x^2 −2+(1/x^2 )))dx−(1/2)∫_0 ^1 (((√2)−(1/x^2 ))/(2x^2 −2+(1/x^2 )))dx =(1/2)∫_0 ^1 (((√2)+(1/x^2 ))/(((√2)x−(1/x))^2 +2(√2)−2))dx−(1/2)∫_0 ^1 (((√2)−(1/x^2 ))/(((√2)x+(1/x))^2 −2(√2)−2))dx =(1/2)∫_(−∞) ^((√2)−1) (du/(u^2 +2(√2)−2))−(1/2)∫_(+∞) ^((√2)+1) (dv/(v^2 −(2(√2)+2))) =(1/(2(√(2(√2)−2))))[arctan((u/( (√(2(√2)−2)))))]_(−∞) ^((√2)−1) +(1/(2(√(2(√2)+2))))[argcoth((v/( (√(2(√2)+2)))))]_(+∞) ^((√2)+1) =(1/(2(√(2((√2)−1)))))[arctan((√(((√2)−1)/( 2))))−(−(π/2))]+(1/( 4(√(2(√2)+2))))[ln∣((v+(√(2(√2)+2)))/(v−(√(2(√2)+2))))∣]_(+∞) ^((√2)+1) =(1/(2(√(2((√2)−1)))))[arctan((√(((√2)−1)/2)))+(π/2)]+(1/(4(√(2(√2)+2))))ln∣(((√2)+1+(√(2(√2)+2)))/( (√2)+1−(√(2(√2)+2))))∣
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\sqrt{\mathrm{2}}{x}^{\mathrm{2}} +\mathrm{1}\right)−\left(\sqrt{\mathrm{2}}{x}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{2}}{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{2}}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left(\sqrt{\mathrm{2}}{x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left(\sqrt{\mathrm{2}}{x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{{du}}{{u}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{+\infty} ^{\sqrt{\mathrm{2}}+\mathrm{1}} \frac{{d}\mathrm{v}}{\mathrm{v}^{\mathrm{2}} −\left(\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}\right)} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}}\left[\mathrm{arctan}\left(\frac{{u}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}}\right)\right]_{−\infty} ^{\sqrt{\mathrm{2}}−\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}}\left[\mathrm{argcoth}\left(\frac{\mathrm{v}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}}\right)\right]_{+\infty} ^{\sqrt{\mathrm{2}}+\mathrm{1}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}}\left[\mathrm{arctan}\left(\sqrt{\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\mathrm{2}}}\right)−\left(−\frac{\pi}{\mathrm{2}}\right)\right]+\frac{\mathrm{1}}{\:\mathrm{4}\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}}\left[\mathrm{ln}\mid\frac{\mathrm{v}+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}}{\mathrm{v}−\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}}\mid\right]_{+\infty} ^{\sqrt{\mathrm{2}}+\mathrm{1}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}}\left[\mathrm{arctan}\left(\sqrt{\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}}}\right)+\frac{\pi}{\mathrm{2}}\right]+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{1}+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}}{\:\sqrt{\mathrm{2}}+\mathrm{1}−\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}}\mid \\ $$
Answered by Ar Brandon last updated on 28/Jan/23
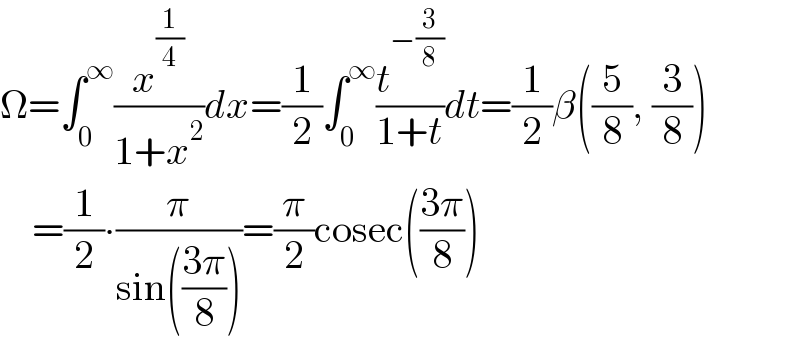
Ω=∫_0 ^∞ (x^(1/4) /(1+x^2 ))dx=(1/2)∫_0 ^∞ (t^(−(3/8)) /(1+t))dt=(1/2)β((5/8), (3/8)) =(1/2)∙(π/(sin(((3π)/8))))=(π/2)cosec(((3π)/8))
$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{−\frac{\mathrm{3}}{\mathrm{8}}} }{\mathrm{1}+{t}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{5}}{\mathrm{8}},\:\frac{\mathrm{3}}{\mathrm{8}}\right) \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\pi}{\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)}=\frac{\pi}{\mathrm{2}}\mathrm{cosec}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$
Answered by cortano1 last updated on 29/Jan/23
(2) ∫_0 ^( ∞) ((x)^(1/4) /(1+x^2 )) dx = ∫_0 ^( ∞) ((4x^4 )/(1+x^8 )) dx = ∫_∞ ^0 ((4x^(−4) )/(x^(−8) +1)) (−x^(−2) dx) = ∫_0 ^( ∞) ((4x^2 )/(1+x^8 )) dx 2I = ∫_0 ^∞ ((4x^4 +4x^2 )/(1+x^8 )) dx I= ∫_0 ^∞ ((2(x^4 +x^2 ))/(1+x^8 )) dx = 2∫_0 ^∞ ((1+x^(−2) )/(x^4 +x^(−4) )) dx I=2∫_0 ^∞ ((d(x−x^(−1) ))/((x^2 +x^(−2) )^2 −2)) I= 2∫_(−∞) ^( ∞) (dt/(t^4 +4t^2 +2)) ; t=x−x^(−1) I= ((√2)/( (√((√2)((√(2+1))))))) [arctan ((w/( (√(4+(√(2(√2))))))))]_(−∞) ^∞ ,w=t−(√2)t^(−1) I=(π/( (√((√2)((√2)+1)))))
$$\left(\mathrm{2}\right)\:\underset{\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\sqrt[{\mathrm{4}}]{{x}}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:=\:\underset{\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{4}{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{8}} }\:{dx} \\ $$$$\:=\:\underset{\infty} {\overset{\mathrm{0}} {\int}}\:\frac{\mathrm{4}{x}^{−\mathrm{4}} }{{x}^{−\mathrm{8}} +\mathrm{1}}\:\left(−{x}^{−\mathrm{2}} \:{dx}\right) \\ $$$$\:=\:\underset{\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{8}} }\:{dx} \\ $$$$\:\mathrm{2}{I}\:=\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{4}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{8}} }\:{dx} \\ $$$${I}=\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{2}\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{8}} }\:{dx}\:=\:\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{1}+{x}^{−\mathrm{2}} }{{x}^{\mathrm{4}} +{x}^{−\mathrm{4}} }\:{dx}\: \\ $$$${I}=\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{d}\left({x}−{x}^{−\mathrm{1}} \right)}{\left({x}^{\mathrm{2}} +{x}^{−\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}} \\ $$$${I}=\:\mathrm{2}\int_{−\infty} ^{\:\infty} \:\frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{2}} +\mathrm{2}}\:;\:{t}={x}−{x}^{−\mathrm{1}} \\ $$$${I}=\:\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\sqrt{\mathrm{2}}\left(\sqrt{\left.\mathrm{2}+\mathrm{1}\right)}\right.}}\:\left[\mathrm{arctan}\:\left(\frac{{w}}{\:\sqrt{\mathrm{4}+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}}}\right)\right]_{−\infty} ^{\infty} ,{w}={t}−\sqrt{\mathrm{2}}{t}^{−\mathrm{1}} \\ $$$${I}=\frac{\pi}{\:\sqrt{\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}}\: \\ $$
Answered by Mathspace last updated on 30/Jan/23
I=∫_0 ^∞ (x^(1/4) /(1+x^2 ))dx (x=t^(1/2) ) =∫_0 ^∞ (t^(1/8) /(1+t)).(1/2)t^(−(1/2)) dt =(1/2)∫_0 ^∞ (t^(−(3/8)) /(1+t))dt =(1/2)∫_0 ^∞ (t^(−(3/8)−1 +1) /(1+t))dt =(1/2)∫_0 ^∞ (t^((5/8)−1) /(1+t))dt=(1/2).(π/(sin(((5π)/8)))) =(π/(2sin((π/2)+(π/8))))=(π/(2cos((π/8)))) =(π/(2.((√(2+(√2)))/2))) =(π/( (√(2+(√2)))))
$${I}=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:\:\:\:\:\:\left({x}={t}^{\frac{\mathrm{1}}{\mathrm{2}}} \right) \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\frac{\mathrm{1}}{\mathrm{8}}} }{\mathrm{1}+{t}}.\frac{\mathrm{1}}{\mathrm{2}}{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{−\frac{\mathrm{3}}{\mathrm{8}}} }{\mathrm{1}+{t}}{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{−\frac{\mathrm{3}}{\mathrm{8}}−\mathrm{1}\:+\mathrm{1}} }{\mathrm{1}+{t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\frac{\mathrm{5}}{\mathrm{8}}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{{sin}\left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)} \\ $$$$=\frac{\pi}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)}=\frac{\pi}{\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{8}}\right)} \\ $$$$=\frac{\pi}{\mathrm{2}.\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}}\:=\frac{\pi}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *