Question Number 59474 by rahul 19 last updated on 10/May/19
![1) ∫_0 ^(10π) ([sec^(−1) x]+[cot^(−1) x] ) dx = ? 2)area bounded by curve y=ln(x) and the lines y=0,y=ln(3) and x=0 is equal to ?](https://www.tinkutara.com/question/Q59474.png)
$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{10}\pi} \left(\left[\mathrm{sec}^{−\mathrm{1}} {x}\right]+\left[\mathrm{co}{t}^{−\mathrm{1}} {x}\right]\:\right)\:{dx}\:=\:? \\ $$$$\left.\mathrm{2}\right){area}\:{bounded}\:{by}\:{curve}\:{y}={ln}\left({x}\right)\:{and} \\ $$$${the}\:{lines}\:{y}=\mathrm{0},{y}={ln}\left(\mathrm{3}\right)\:{and}\:{x}=\mathrm{0}\:{is} \\ $$$${equal}\:{to}\:? \\ $$
Commented by tanmay last updated on 10/May/19
![1) from graph it cleaer now... [cot^(−1) x]=0 when x [0,10π] ∫_0 ^(10π) [sec^(−1) x]dx+∫_0 ^(10π) [cot^(−1) x]dx ∫_0 ^(sec1) [sec^(−1) x]dx+∫_(sec1) ^(10π) [sec^(−1) x]dx =∫_0 ^(sec1) 0×dx+∫_(sec1) ^(10π) 1×dx =0+(10π−sec1) =10π−sec1](https://www.tinkutara.com/question/Q59492.png)
$$\left.\mathrm{1}\right)\:{from}\:{graph}\:{it}\:{cleaer}\:{now}… \\ $$$$\left[{cot}^{−\mathrm{1}} {x}\right]=\mathrm{0}\:\:\:\:{when}\:{x}\:\left[\mathrm{0},\mathrm{10}\pi\right] \\ $$$$\int_{\mathrm{0}} ^{\mathrm{10}\pi} \left[{sec}^{−\mathrm{1}} {x}\right]{dx}+\int_{\mathrm{0}} ^{\mathrm{10}\pi} \left[{cot}^{−\mathrm{1}} {x}\right]{dx} \\ $$$$\int_{\mathrm{0}} ^{{sec}\mathrm{1}} \left[{sec}^{−\mathrm{1}} {x}\right]{dx}+\int_{{sec}\mathrm{1}} ^{\mathrm{10}\pi} \left[{sec}^{−\mathrm{1}} {x}\right]{dx} \\ $$$$=\int_{\mathrm{0}} ^{{sec}\mathrm{1}} \mathrm{0}×{dx}+\int_{{sec}\mathrm{1}} ^{\mathrm{10}\pi} \mathrm{1}×{dx} \\ $$$$=\mathrm{0}+\left(\mathrm{10}\pi−{sec}\mathrm{1}\right) \\ $$$$=\mathrm{10}\pi−{sec}\mathrm{1} \\ $$
Commented by tanmay last updated on 10/May/19

Commented by tanmay last updated on 10/May/19

Answered by tanmay last updated on 10/May/19
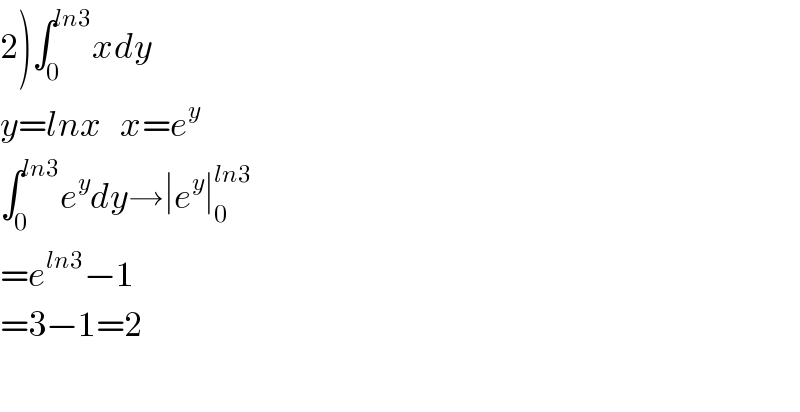
$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{{ln}\mathrm{3}} {xdy} \\ $$$${y}={lnx}\:\:\:{x}={e}^{{y}} \\ $$$$\int_{\mathrm{0}} ^{{ln}\mathrm{3}} {e}^{{y}} {dy}\rightarrow\mid{e}^{{y}} \mid_{\mathrm{0}} ^{{ln}\mathrm{3}} \\ $$$$={e}^{{ln}\mathrm{3}} −\mathrm{1} \\ $$$$=\mathrm{3}−\mathrm{1}=\mathrm{2} \\ $$$$ \\ $$
Commented by tanmay last updated on 10/May/19

$${ans}\:{of}\:\mathrm{2}\:{pls}\:{check} \\ $$
Commented by rahul 19 last updated on 10/May/19

$${thanks}\:{sir}. \\ $$
