Question Number 149625 by puissant last updated on 06/Aug/21
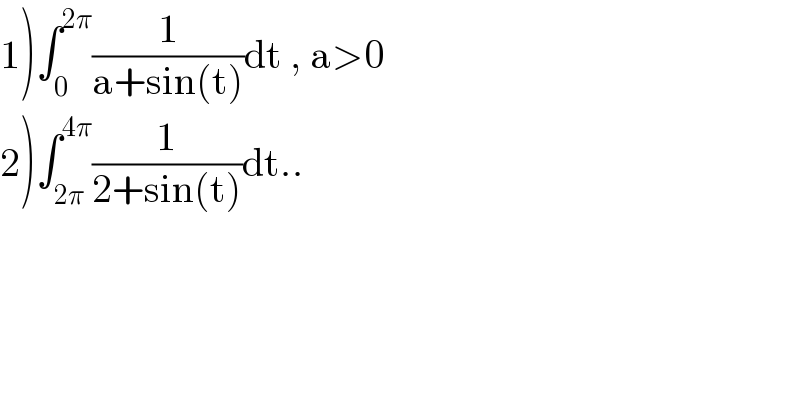
$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{\mathrm{a}+\mathrm{sin}\left(\mathrm{t}\right)}\mathrm{dt}\:,\:\mathrm{a}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{2}\pi} ^{\mathrm{4}\pi} \frac{\mathrm{1}}{\mathrm{2}+\mathrm{sin}\left(\mathrm{t}\right)}\mathrm{dt}.. \\ $$
Answered by ArielVyny last updated on 06/Aug/21
![∫_0 ^(2π) (1/(a+sint))dt posons t=tan((x/2))→sint=((2t)/(1+t^2 )) 2dt=(1+t^2 )dx→dx=(2/(1+t^2 ))dt 2π=tan((x/2))→x=2arctg(2π) ∫_0 ^(2arctg(2π)) (1/(a+((2t)/(1+t^2 ))))×(2/(1+t^2 ))dt ∫_0 ^(2arctg(2π)) (2/(a(1+t^2 )+2t))dt=2∫_0 ^(2arctg(2π)) (1/(at^2 +2t+a)) 2∫_0 ^(2arctg(2π)) (1/(a[(t+(2/a))^2 −(4/a^2 )+(a^2 /a^2 )]))dt (2/a)∫_0 ^(2arctg(2π)) (1/([(t+(2/a))^2 +((a^2 −4)/a^2 )]))dt (2/a)∫_0 ^(2arctg(2π)) (1/((((a^2 −4)/a^2 ))[1+(a^2 /(a^2 −4))(t+(2/a))^2 ]))dt (2/a)×(a^2 /(a^2 −4))∫_0 ^(2arctg(2π)) (1/(1+(a^2 /(a^2 −4))(t+(2/a))^2 )) (2/a)∫_0 ^(2arctg(2π)) (a^2 /(a^2 −4))(1/(1+[(√((a^2 /(a^2 −4))(t+(2/a))))]^2 ))dt (2/a)arctg[((a^2 /(a^2 −4)))(2arctg(2π)+(2/a))] a>0](https://www.tinkutara.com/question/Q149627.png)
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{{a}+{sint}}{dt} \\ $$$${posons}\:{t}={tan}\left(\frac{{x}}{\mathrm{2}}\right)\rightarrow{sint}=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\mathrm{2}{dt}=\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dx}\rightarrow{dx}=\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\mathrm{2}\pi={tan}\left(\frac{{x}}{\mathrm{2}}\right)\rightarrow{x}=\mathrm{2}{arctg}\left(\mathrm{2}\pi\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}{arctg}\left(\mathrm{2}\pi\right)} \frac{\mathrm{1}}{{a}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}{arctg}\left(\mathrm{2}\pi\right)} \frac{\mathrm{2}}{{a}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\mathrm{2}{t}}{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}{arctg}\left(\mathrm{2}\pi\right)} \frac{\mathrm{1}}{{at}^{\mathrm{2}} +\mathrm{2}{t}+{a}} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}{arctg}\left(\mathrm{2}\pi\right)} \frac{\mathrm{1}}{{a}\left[\left({t}+\frac{\mathrm{2}}{{a}}\right)^{\mathrm{2}} −\frac{\mathrm{4}}{{a}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right]}{dt} \\ $$$$\frac{\mathrm{2}}{{a}}\int_{\mathrm{0}} ^{\mathrm{2}{arctg}\left(\mathrm{2}\pi\right)} \frac{\mathrm{1}}{\left[\left({t}+\frac{\mathrm{2}}{{a}}\right)^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} −\mathrm{4}}{{a}^{\mathrm{2}} }\right]}{dt} \\ $$$$\frac{\mathrm{2}}{{a}}\int_{\mathrm{0}} ^{\mathrm{2}{arctg}\left(\mathrm{2}\pi\right)} \frac{\mathrm{1}}{\left(\frac{{a}^{\mathrm{2}} −\mathrm{4}}{{a}^{\mathrm{2}} }\right)\left[\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{4}}\left({t}+\frac{\mathrm{2}}{{a}}\right)^{\mathrm{2}} \right]}{dt} \\ $$$$\frac{\mathrm{2}}{{a}}×\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{2}{arctg}\left(\mathrm{2}\pi\right)} \frac{\mathrm{1}}{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{4}}\left({t}+\frac{\mathrm{2}}{{a}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}}{{a}}\int_{\mathrm{0}} ^{\mathrm{2}{arctg}\left(\mathrm{2}\pi\right)} \frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{4}}\frac{\mathrm{1}}{\mathrm{1}+\left[\sqrt{\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{4}}\left({t}+\frac{\mathrm{2}}{{a}}\right)}\right]^{\mathrm{2}} }{dt} \\ $$$$\frac{\mathrm{2}}{{a}}{arctg}\left[\left(\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{4}}\right)\left(\mathrm{2}{arctg}\left(\mathrm{2}\pi\right)+\frac{\mathrm{2}}{{a}}\right)\right]\:{a}>\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
Commented by ArielVyny last updated on 06/Aug/21

$${peut}-{etre}\:{ma}\:{methode}\:{est}\:{un}\:{peu}\:{drastique} \\ $$$${je}\:{vais}\:{voir}\:{une}\:{autre}\:{approche} \\ $$
Commented by ArielVyny last updated on 06/Aug/21
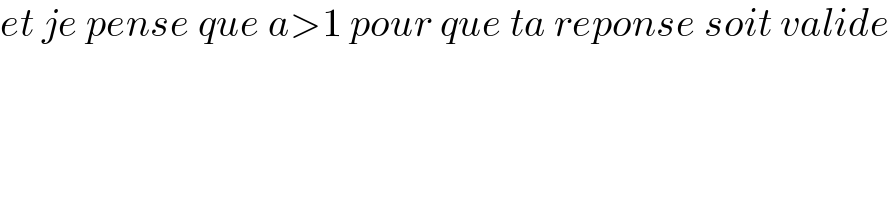
$${et}\:{je}\:{pense}\:{que}\:{a}>\mathrm{1}\:{pour}\:{que}\:{ta}\:{reponse}\:{soit}\:{valide} \\ $$
