Question Number 106570 by bobhans last updated on 06/Aug/20
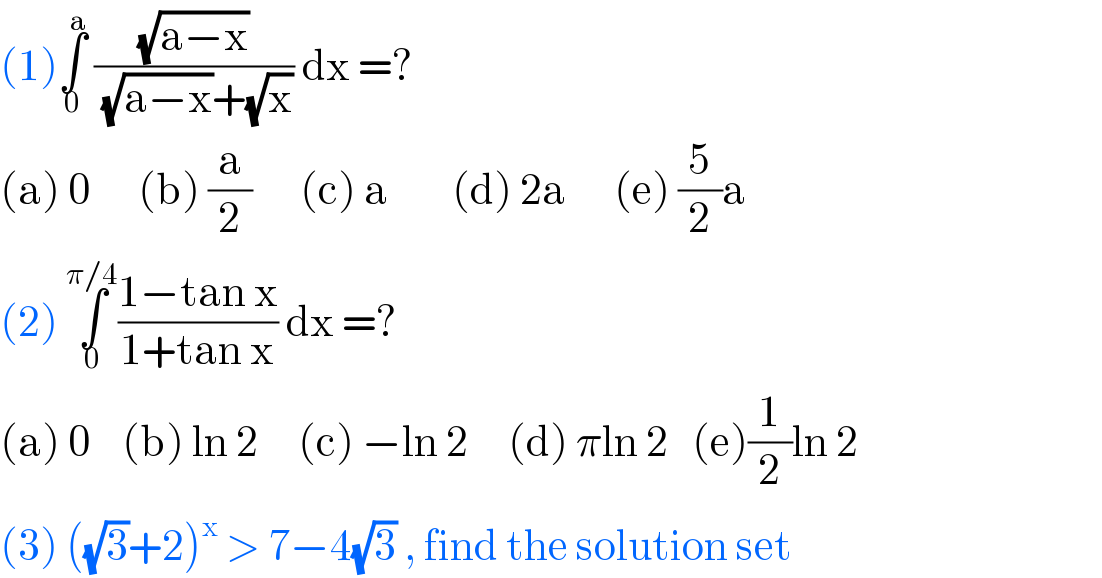
$$\left(\mathrm{1}\right)\underset{\mathrm{0}} {\overset{\mathrm{a}} {\int}}\:\frac{\sqrt{\mathrm{a}−\mathrm{x}}}{\:\sqrt{\mathrm{a}−\mathrm{x}}+\sqrt{\mathrm{x}}}\:\mathrm{dx}\:=? \\ $$$$\left(\mathrm{a}\right)\:\mathrm{0}\:\:\:\:\:\:\left(\mathrm{b}\right)\:\frac{\mathrm{a}}{\mathrm{2}}\:\:\:\:\:\:\left(\mathrm{c}\right)\:\mathrm{a}\:\:\:\:\:\:\:\:\left(\mathrm{d}\right)\:\mathrm{2a}\:\:\:\:\:\:\left(\mathrm{e}\right)\:\frac{\mathrm{5}}{\mathrm{2}}\mathrm{a} \\ $$$$\left(\mathrm{2}\right)\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\frac{\mathrm{1}−\mathrm{tan}\:\mathrm{x}}{\mathrm{1}+\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx}\:=? \\ $$$$\left(\mathrm{a}\right)\:\mathrm{0}\:\:\:\:\left(\mathrm{b}\right)\:\mathrm{ln}\:\mathrm{2}\:\:\:\:\:\left(\mathrm{c}\right)\:−\mathrm{ln}\:\mathrm{2}\:\:\:\:\:\left(\mathrm{d}\right)\:\pi\mathrm{ln}\:\mathrm{2}\:\:\:\left(\mathrm{e}\right)\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2} \\ $$$$\left(\mathrm{3}\right)\:\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)^{\mathrm{x}} \:>\:\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\:,\:\mathrm{find}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{set} \\ $$
Answered by bemath last updated on 06/Aug/20
![(2) ((1−tan x)/(1+tan x)) = ((cos x−sin x)/(cos x+sin x)) = ((1−sin 2x)/(cos 2x)) = sec 2x−tan 2x ∫_0 ^(π/4) (sec 2x−tan 2x)dx = [(1/2)ln ∣sec 2x−tan 2x∣−(1/2)ln ∣cos 2x∣ ]_( 0) ^(π/4) = ln 2](https://www.tinkutara.com/question/Q106574.png)
$$\left(\mathrm{2}\right)\:\frac{\mathrm{1}−\mathrm{tan}\:\mathrm{x}}{\mathrm{1}+\mathrm{tan}\:\mathrm{x}}\:=\:\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}} \\ $$$$\:\:\:=\:\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{2x}}{\mathrm{cos}\:\mathrm{2x}}\:=\:\mathrm{sec}\:\mathrm{2x}−\mathrm{tan}\:\mathrm{2x} \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\left(\mathrm{sec}\:\mathrm{2x}−\mathrm{tan}\:\mathrm{2x}\right)\mathrm{dx}\:= \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{2x}−\mathrm{tan}\:\mathrm{2x}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{cos}\:\mathrm{2x}\mid\:\right]_{\:\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\:\mathrm{ln}\:\mathrm{2} \\ $$
Answered by john santu last updated on 06/Aug/20
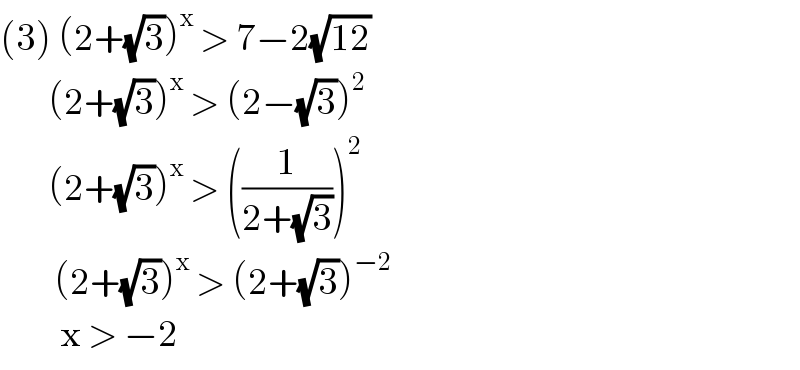
$$\left(\mathrm{3}\right)\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:>\:\mathrm{7}−\mathrm{2}\sqrt{\mathrm{12}} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:>\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:>\:\left(\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \:>\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{−\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:>\:−\mathrm{2}\: \\ $$
Answered by Dwaipayan Shikari last updated on 06/Aug/20
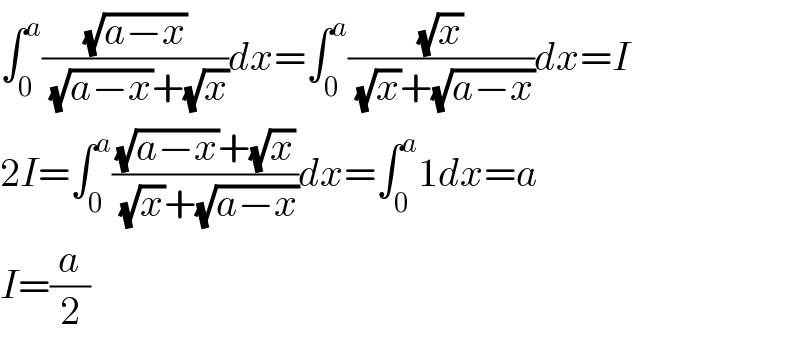
$$\int_{\mathrm{0}} ^{{a}} \frac{\sqrt{{a}−{x}}}{\:\sqrt{{a}−{x}}+\sqrt{{x}}}{dx}=\int_{\mathrm{0}} ^{{a}} \frac{\sqrt{{x}}}{\:\sqrt{{x}}+\sqrt{{a}−{x}}}{dx}={I} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{{a}} \frac{\sqrt{{a}−{x}}+\sqrt{{x}}}{\:\sqrt{{x}}+\sqrt{{a}−{x}}}{dx}=\int_{\mathrm{0}} ^{{a}} \mathrm{1}{dx}={a} \\ $$$${I}=\frac{{a}}{\mathrm{2}} \\ $$
