Question Number 59040 by rahul 19 last updated on 03/May/19
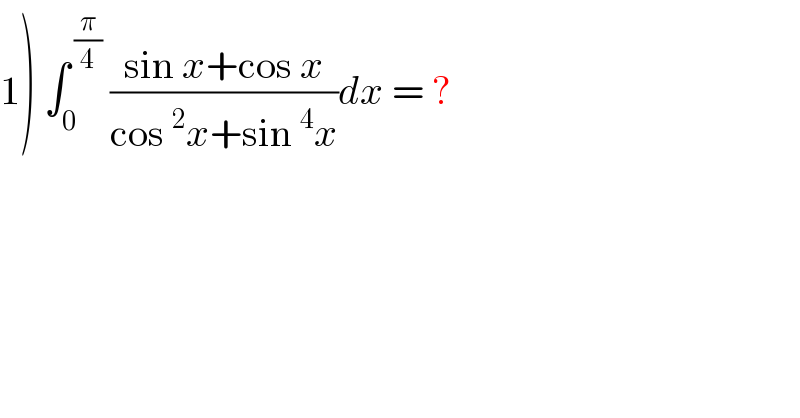
$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{sin}\:^{\mathrm{4}} {x}}{dx}\:=\:? \\ $$
Answered by tanmay last updated on 03/May/19
![1)∫((sinxdx)/(cos^2 x+(1−cos^2 x)^2 ))+∫((cosxdx)/(1−sin^2 x+sin^4 x)) ∫((−da)/(a^2 +1−2a^2 +a^4 ))+∫(db/(1−b^2 +b^4 )) =−I_1 +I_2 calculation of −I_1 (−1)∫((1/a^2 )/((1/a^2 )−1+a^2 ))da (−(1/2))∫(((1+(1/a^2 ))−(1−(1/a^2 )))/(a^2 +(1/a^2 )−1))da =(1/2)[∫((1−(1/a^2 ))/(a^2 +(1/a^2 )−1))da−∫((1+(1/a^2 ))/(a^2 +(1/a^2 )−1))da] =(1/2)[∫((d(a+(1/a)))/((a+(1/a))^2 −3))−∫((d(a−(1/a)))/((a−(1/a))^2 +1))] =(1/2)[(1/(2(√3)))ln(((a+(1/a)−(√3))/(a+(1/a)+(√3))))−tan^(−1) (a−(1/a))] =∣(1/2)[(1/(2(√3)))ln(((cosx+secx−(√3))/(cosx+secx+(√3))))−tan^(−1) (cosx−secx)]∣_0 ^(π/4) now calculation of I_2 ∫(db/(b^4 −b^2 +1)) =(1/2)∫((2/b^2 )/(b^2 +(1/b^2 )−1))db =(1/(2 ))∫(((1+(1/b^2 ))−(1−(1/b^2 )))/(b^2 +(1/b^2 )−1))db =(1/2)[∫((d(b−(1/b)))/((b−(1/b))^2 +1))−∫((d(b+(1/b)))/((b+(1/b))^2 −3))] =(1/2)[tan^(−1) (b−(1/b))−(1/(2(√3)))ln(((b+(1/b)−(√3))/(b+(1/b)+(√3))))] =(1/2)∣[tan^(−1) (sinx−cosecx)−(1/(2(√3)))ln(((sinx+cosecx−(√3))/(sinx+cosecx+(√3))))]∣_0 ^(π/4) Rahul pls check...lenthy problem...mistake if any](https://www.tinkutara.com/question/Q59043.png)
$$\left.\mathrm{1}\right)\int\frac{{sinxdx}}{{cos}^{\mathrm{2}} {x}+\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }+\int\frac{{cosxdx}}{\mathrm{1}−{sin}^{\mathrm{2}} {x}+{sin}^{\mathrm{4}} {x}} \\ $$$$\int\frac{−{da}}{{a}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{a}^{\mathrm{2}} +{a}^{\mathrm{4}} }+\int\frac{{db}}{\mathrm{1}−{b}^{\mathrm{2}} +{b}^{\mathrm{4}} } \\ $$$$=−{I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$${calculation}\:{of}\:−{I}_{\mathrm{1}} \\ $$$$\left(−\mathrm{1}\right)\int\frac{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }}{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\mathrm{1}+{a}^{\mathrm{2}} }{da} \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)}{{a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\mathrm{1}}{da} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\mathrm{1}}{da}−\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\mathrm{1}}{da}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{{d}\left({a}+\frac{\mathrm{1}}{{a}}\right)}{\left({a}+\frac{\mathrm{1}}{{a}}\right)^{\mathrm{2}} −\mathrm{3}}−\int\frac{{d}\left({a}−\frac{\mathrm{1}}{{a}}\right)}{\left({a}−\frac{\mathrm{1}}{{a}}\right)^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{ln}\left(\frac{{a}+\frac{\mathrm{1}}{{a}}−\sqrt{\mathrm{3}}}{{a}+\frac{\mathrm{1}}{{a}}+\sqrt{\mathrm{3}}}\right)−{tan}^{−\mathrm{1}} \left({a}−\frac{\mathrm{1}}{{a}}\right)\right] \\ $$$$=\mid\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{ln}\left(\frac{{cosx}+{secx}−\sqrt{\mathrm{3}}}{{cosx}+{secx}+\sqrt{\mathrm{3}}}\right)−{tan}^{−\mathrm{1}} \left({cosx}−{secx}\right)\right]\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${now}\:{calculation}\:{of}\:{I}_{\mathrm{2}} \\ $$$$\int\frac{{db}}{{b}^{\mathrm{4}} −{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\frac{\mathrm{2}}{{b}^{\mathrm{2}} }}{{b}^{\mathrm{2}} +\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\mathrm{1}}{db} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\:}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)}{{b}^{\mathrm{2}} +\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\mathrm{1}}{db} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{{d}\left({b}−\frac{\mathrm{1}}{{b}}\right)}{\left({b}−\frac{\mathrm{1}}{{b}}\right)^{\mathrm{2}} +\mathrm{1}}−\int\frac{{d}\left({b}+\frac{\mathrm{1}}{{b}}\right)}{\left({b}+\frac{\mathrm{1}}{{b}}\right)^{\mathrm{2}} −\mathrm{3}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{tan}^{−\mathrm{1}} \left({b}−\frac{\mathrm{1}}{{b}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{ln}\left(\frac{{b}+\frac{\mathrm{1}}{{b}}−\sqrt{\mathrm{3}}}{{b}+\frac{\mathrm{1}}{{b}}+\sqrt{\mathrm{3}}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mid\left[{tan}^{−\mathrm{1}} \left({sinx}−{cosecx}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{ln}\left(\frac{{sinx}+{cosecx}−\sqrt{\mathrm{3}}}{{sinx}+{cosecx}+\sqrt{\mathrm{3}}}\right)\right]\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$ \\ $$$${Rahul}\:{pls}\:{check}…{lenthy}\:{problem}…{mistake}\:{if}\:{any} \\ $$
Commented by rahul 19 last updated on 04/May/19

$${thank}\:{You}\:{Sir}. \\ $$
Answered by MJS last updated on 03/May/19
![∫_0 ^(π/4) ((cos x)/(cos^2 x +sin^4 x))dx= [t=sin x → dx=(dt/(cos x))] =∫_0 ^((√2)/2) (dt/(t^4 −t^2 +1))=∫_0 ^((√2)/2) (dt/((t^2 −(√3)t+1)(t^2 +(√3)t+1))) ∫_0 ^(π/4) ((sin x)/(cos^2 x +sin^4 x))dx= [u=cos x → dx=−(du/(sin x))] =−∫_1 ^((√2)/2) (du/(u^4 −u^2 +1)) ⇒ we only have to solve the 1^(st) one ∫(dt/((t^2 −(√3)t+1)(t^2 +(√3)t+1)))= =∫(((1/2)−((√3)/6)t)/(t^2 −(√3)t+1))dt+∫(((1/2)+((√3)/6)t)/(t^2 +(√3)t+1))dt= =−((√3)/6)∫((t−(√3))/(t^2 −(√3)t+1))dt+((√3)/6)∫((t+(√3))/(t^2 +(√3)t+1))dt= =(1/2)arctan (2t−(√3)) −((√3)/(12))ln (t^2 −(√3)t+1) +(1/2)arctan (2t+(√3)) +((√3)/(12))ln (t^2 +(√3)t+1) now please finish it, Sir Rahul, I have to go to bed...](https://www.tinkutara.com/question/Q59044.png)
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\frac{\mathrm{cos}\:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}\:+\mathrm{sin}^{\mathrm{4}} \:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sin}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{cos}\:{x}}\right] \\ $$$$=\underset{\mathrm{0}} {\overset{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} {\int}}\frac{{dt}}{{t}^{\mathrm{4}} −{t}^{\mathrm{2}} +\mathrm{1}}=\underset{\mathrm{0}} {\overset{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} {\int}}\frac{{dt}}{\left({t}^{\mathrm{2}} −\sqrt{\mathrm{3}}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\sqrt{\mathrm{3}}{t}+\mathrm{1}\right)} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\frac{\mathrm{sin}\:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}\:+\mathrm{sin}^{\mathrm{4}} \:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{cos}\:{x}\:\rightarrow\:{dx}=−\frac{{du}}{\mathrm{sin}\:{x}}\right] \\ $$$$=−\underset{\mathrm{1}} {\overset{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} {\int}}\frac{{du}}{{u}^{\mathrm{4}} −{u}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow\:\mathrm{we}\:\mathrm{only}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{one} \\ $$$$ \\ $$$$\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\sqrt{\mathrm{3}}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\sqrt{\mathrm{3}}{t}+\mathrm{1}\right)}= \\ $$$$=\int\frac{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}{t}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{3}}{t}+\mathrm{1}}{dt}+\int\frac{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}{t}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{3}}{t}+\mathrm{1}}{dt}= \\ $$$$=−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{t}−\sqrt{\mathrm{3}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{3}}{t}+\mathrm{1}}{dt}+\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{t}+\sqrt{\mathrm{3}}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{3}}{t}+\mathrm{1}}{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\left(\mathrm{2}{t}−\sqrt{\mathrm{3}}\right)\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\mathrm{ln}\:\left({t}^{\mathrm{2}} −\sqrt{\mathrm{3}}{t}+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\left(\mathrm{2}{t}+\sqrt{\mathrm{3}}\right)\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\sqrt{\mathrm{3}}{t}+\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{please}\:\mathrm{finish}\:\mathrm{it},\:\mathrm{Sir}\:\mathrm{Rahul},\:\mathrm{I}\:\mathrm{have}\:\mathrm{to}\:\mathrm{go} \\ $$$$\mathrm{to}\:\mathrm{bed}… \\ $$
Commented by MJS last updated on 03/May/19
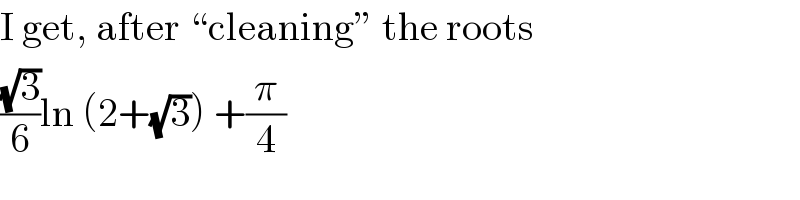
$$\mathrm{I}\:\mathrm{get},\:\mathrm{after}\:“\mathrm{cleaning}''\:\mathrm{the}\:\mathrm{roots} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\:+\frac{\pi}{\mathrm{4}} \\ $$
Commented by rahul 19 last updated on 04/May/19

$${thank}\:{you}\:{sir}. \\ $$
Answered by MJS last updated on 04/May/19
![I found another path ∫((sin x +cos x)/(cos^2 x +sin^4 x))dx=8(√2)∫((sin (x+(π/4)))/(7+cos 4x))dx= [t=cos (x+(π/4)) → dx=−(dt/(sin (x+(π/4))))] =4(√2)∫(dt/(4t^4 −4t^2 +1))=4(√2)∫(dt/((2t^2 −3)(2t^2 +1)))= =((√6)/6)∫(dt/( (√2)t−(√3)))−((√6)/6)∫(dt/( (√2)t+(√3)))−(√2)∫(dt/(2t^2 +1))= =((√3)/6)ln (((√2)t−(√3))/( (√2)t+(√3))) −arctan (√2)t = =((√3)/6)ln (((2t−(√6))^2 )/(2(2t^2 −3))) −arctan (√2)t= =((√3)/3)ln (2t−(√6)) −((√3)/6)ln (2t^2 −3) −((√3)/6)ln 2 −arctan (√2)t= =((√3)/3)ln ∣2t−(√6)∣ −((√3)/6)ln ∣2t^2 −3∣ −arctan (√2)t +C the borders [0≤x≤(π/4)] → [((√2)/2)≥t≥0] ⇒ ∫_0 ^(π/4) ((sin x +cos x)/(cos^2 x +sin^4 x))dx=(π/4)−((√3)/6)ln (2−(√3))](https://www.tinkutara.com/question/Q59081.png)
$$\mathrm{I}\:\mathrm{found}\:\mathrm{another}\:\mathrm{path} \\ $$$$\int\frac{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}\:+\mathrm{sin}^{\mathrm{4}} \:{x}}{dx}=\mathrm{8}\sqrt{\mathrm{2}}\int\frac{\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{7}+\mathrm{cos}\:\mathrm{4}{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\:\rightarrow\:{dx}=−\frac{{dt}}{\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}\right] \\ $$$$=\mathrm{4}\sqrt{\mathrm{2}}\int\frac{{dt}}{\mathrm{4}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{4}\sqrt{\mathrm{2}}\int\frac{{dt}}{\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\right)\left(\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right)}= \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{6}}\int\frac{{dt}}{\:\sqrt{\mathrm{2}}{t}−\sqrt{\mathrm{3}}}−\frac{\sqrt{\mathrm{6}}}{\mathrm{6}}\int\frac{{dt}}{\:\sqrt{\mathrm{2}}{t}+\sqrt{\mathrm{3}}}−\sqrt{\mathrm{2}}\int\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}}{t}−\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}{t}+\sqrt{\mathrm{3}}}\:−\mathrm{arctan}\:\sqrt{\mathrm{2}}{t}\:= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\frac{\left(\mathrm{2}{t}−\sqrt{\mathrm{6}}\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\right)}\:−\mathrm{arctan}\:\sqrt{\mathrm{2}}{t}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{ln}\:\left(\mathrm{2}{t}−\sqrt{\mathrm{6}}\right)\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\right)\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\mathrm{2}\:−\mathrm{arctan}\:\sqrt{\mathrm{2}}{t}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{ln}\:\mid\mathrm{2}{t}−\sqrt{\mathrm{6}}\mid\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\mid\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\mid\:−\mathrm{arctan}\:\sqrt{\mathrm{2}}{t}\:+{C} \\ $$$$\mathrm{the}\:\mathrm{borders}\:\left[\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{4}}\right]\:\rightarrow\:\left[\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\geqslant{t}\geqslant\mathrm{0}\right] \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\frac{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}\:+\mathrm{sin}^{\mathrm{4}} \:{x}}{dx}=\frac{\pi}{\mathrm{4}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$
Commented by MJS last updated on 04/May/19
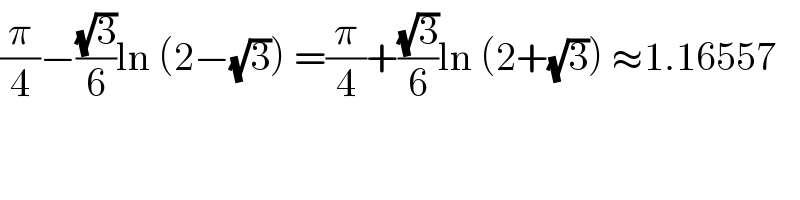
$$\frac{\pi}{\mathrm{4}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\:=\frac{\pi}{\mathrm{4}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\:\approx\mathrm{1}.\mathrm{16557} \\ $$
