Question Number 113910 by bobhans last updated on 16/Sep/20
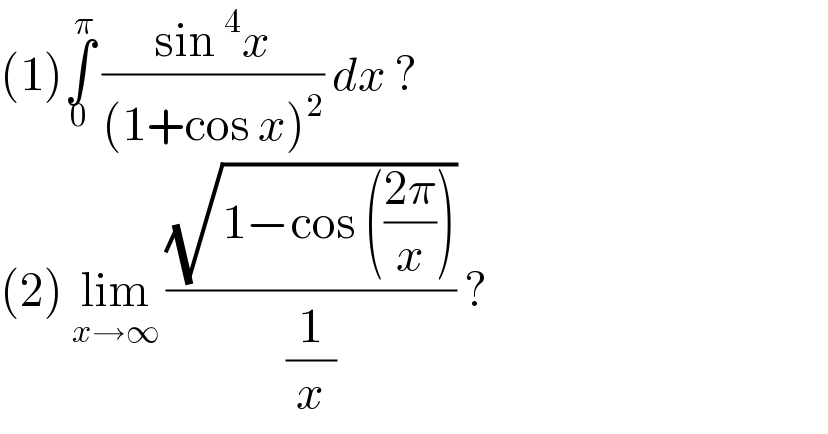
$$\left(\mathrm{1}\right)\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{sin}\:^{\mathrm{4}} {x}}{\left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:{dx}\:? \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{{x}}\right)}}{\frac{\mathrm{1}}{{x}}}\:? \\ $$
Answered by bemath last updated on 16/Sep/20
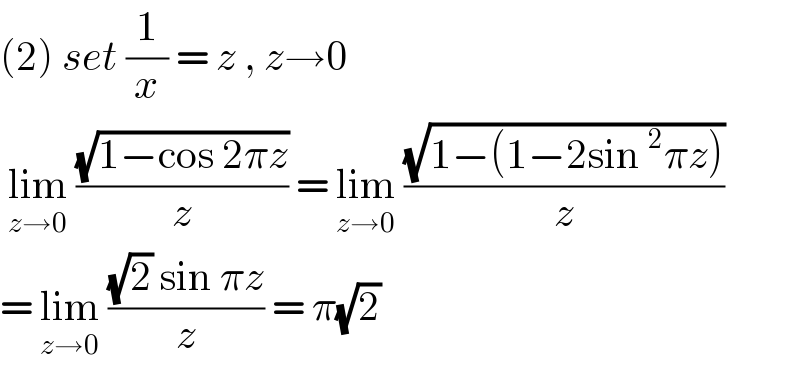
$$\left(\mathrm{2}\right)\:{set}\:\frac{\mathrm{1}}{{x}}\:=\:{z}\:,\:{z}\rightarrow\mathrm{0} \\ $$$$\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\pi{z}}}{{z}}\:=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \pi{z}\right)}}{{z}} \\ $$$$=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\pi{z}}{{z}}\:=\:\pi\sqrt{\mathrm{2}} \\ $$
Answered by 1549442205PVT last updated on 16/Sep/20
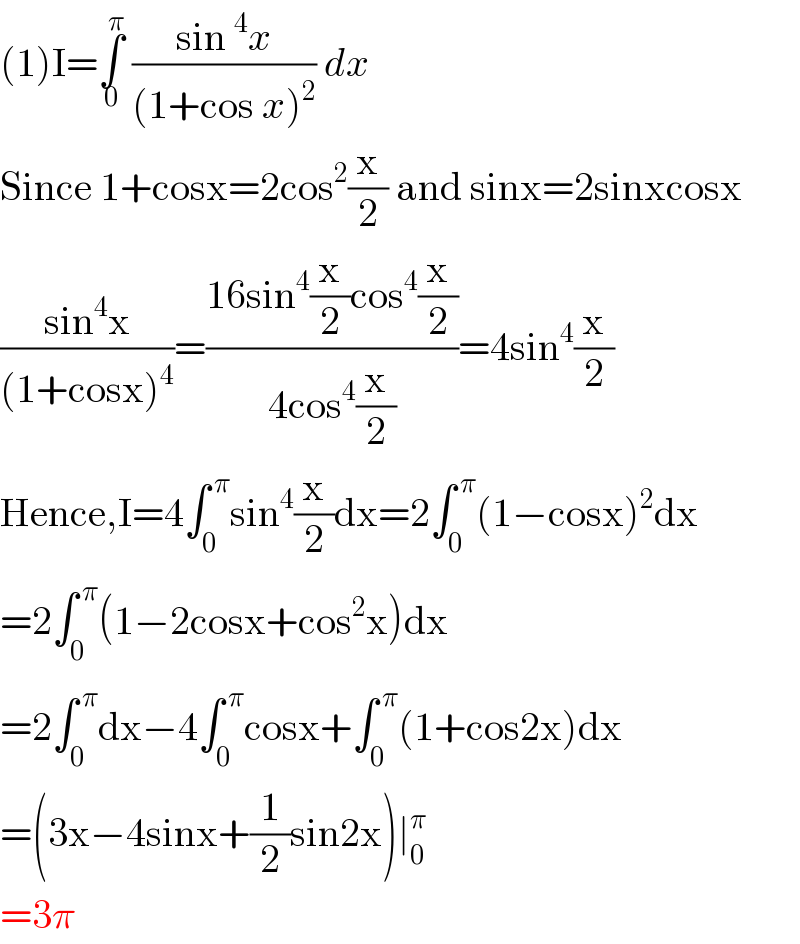
$$\left(\mathrm{1}\right)\mathrm{I}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{sin}\:^{\mathrm{4}} {x}}{\left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:{dx}\: \\ $$$$\mathrm{Since}\:\mathrm{1}+\mathrm{cosx}=\mathrm{2cos}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{sinx}=\mathrm{2sinxcosx} \\ $$$$\frac{\mathrm{sin}^{\mathrm{4}} \mathrm{x}}{\left(\mathrm{1}+\mathrm{cosx}\right)^{\mathrm{4}} }=\frac{\mathrm{16sin}^{\mathrm{4}} \frac{\mathrm{x}}{\mathrm{2}}\mathrm{cos}^{\mathrm{4}} \frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{4cos}^{\mathrm{4}} \frac{\mathrm{x}}{\mathrm{2}}}=\mathrm{4sin}^{\mathrm{4}} \frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\mathrm{Hence},\mathrm{I}=\mathrm{4}\int_{\mathrm{0}} ^{\:\pi} \mathrm{sin}^{\mathrm{4}} \frac{\mathrm{x}}{\mathrm{2}}\mathrm{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\:\pi} \left(\mathrm{1}−\mathrm{cosx}\right)^{\mathrm{2}} \mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\:\pi} \left(\mathrm{1}−\mathrm{2cosx}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\:\pi} \mathrm{dx}−\mathrm{4}\int_{\mathrm{0}} ^{\:\pi} \mathrm{cosx}+\int_{\mathrm{0}} ^{\:\pi} \left(\mathrm{1}+\mathrm{cos2x}\right)\mathrm{dx} \\ $$$$=\left(\mathrm{3x}−\mathrm{4sinx}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2x}\right)\mid_{\mathrm{0}} ^{\pi} \\ $$$$=\mathrm{3}\pi \\ $$
Answered by MJS_new last updated on 16/Sep/20
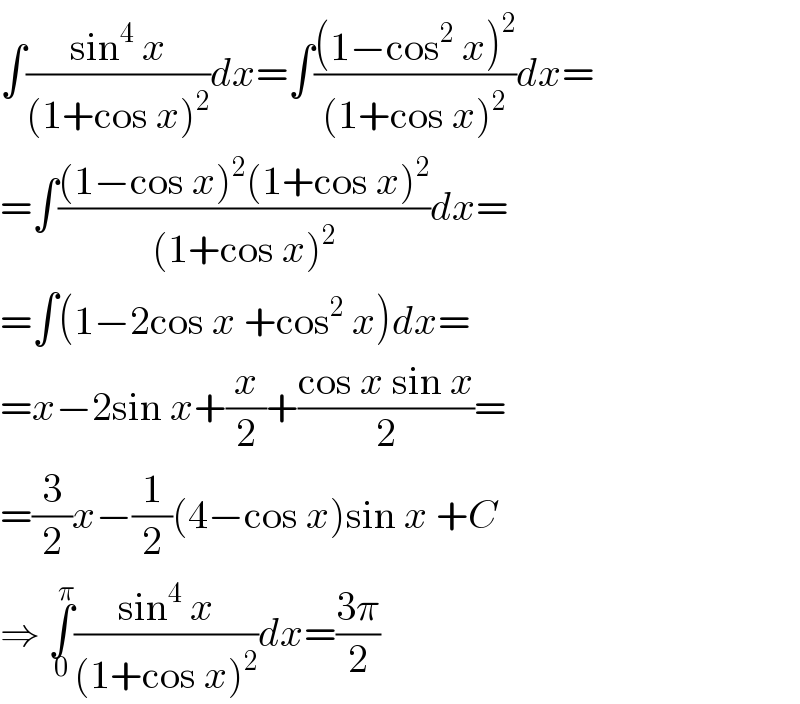
$$\int\frac{\mathrm{sin}^{\mathrm{4}} \:{x}}{\left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{dx}=\int\frac{\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{x}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\int\frac{\left(\mathrm{1}−\mathrm{cos}\:{x}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\int\left(\mathrm{1}−\mathrm{2cos}\:{x}\:+\mathrm{cos}^{\mathrm{2}} \:{x}\right){dx}= \\ $$$$={x}−\mathrm{2sin}\:{x}+\frac{{x}}{\mathrm{2}}+\frac{\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}}{\mathrm{2}}= \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}−\mathrm{cos}\:{x}\right)\mathrm{sin}\:{x}\:+{C} \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{sin}^{\mathrm{4}} \:{x}}{\left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{dx}=\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 17/Sep/20
![1) A =∫_0 ^π ((sin^4 x)/((1+cosx)^2 ))dx ⇒A =∫_0 ^π (((2sin((x/2))cos((x/2)))^4 )/((2cos^2 ((x/2)))^2 )) dx =4∫_0 ^π ((sin^4 ((x/2)) cos^4 ((x/2)))/(cos^4 ((x/2)))) dx =4 ∫_0 ^π sin^4 ((x/2))dx =_((x/2)=t) 8∫_0 ^(π/2) sin^4 (t) dt =8 ∫_0 ^(π/2) (((1−cos(2t))/2))^2 dt =2 ∫_0 ^(π/2) (1−2cos(2t) +cos^2 (2t))dt =2 [t−sin(2t)]_0 ^(π/2) +∫_0 ^(π/2) (1+cos(4t))dt =2{(π/2)} +(π/2) =π +(π/2) ⇒A =((3π)/2)](https://www.tinkutara.com/question/Q114057.png)
$$\left.\mathrm{1}\right)\:\mathrm{A}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{sin}^{\mathrm{4}} \mathrm{x}}{\left(\mathrm{1}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{A}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\left(\mathrm{2sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)^{\mathrm{4}} }{\left(\mathrm{2cos}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{sin}^{\mathrm{4}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:\mathrm{cos}^{\mathrm{4}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{cos}^{\mathrm{4}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}\:\mathrm{dx}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{sin}^{\mathrm{4}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$=_{\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t}} \:\:\:\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{4}} \left(\mathrm{t}\right)\:\mathrm{dt}\:=\mathrm{8}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}\right)^{\mathrm{2}} \:\mathrm{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{2cos}\left(\mathrm{2t}\right)\:+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{2t}\right)\right)\mathrm{dt} \\ $$$$=\mathrm{2}\:\left[\mathrm{t}−\mathrm{sin}\left(\mathrm{2t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{4t}\right)\right)\mathrm{dt} \\ $$$$=\mathrm{2}\left\{\frac{\pi}{\mathrm{2}}\right\}\:+\frac{\pi}{\mathrm{2}}\:=\pi\:+\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{A}\:=\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$
