Question Number 52515 by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19

$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−\mathrm{1}} \left({ax}\right)−{tan}^{−\mathrm{1}} \left({bx}\right)}{{x}}{dx} \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} {sinx}}{{x}}{dx} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jan/19

$${thank}\:{you}\:{sir}… \\ $$
Commented by maxmathsup by imad last updated on 09/Jan/19
![1) let I(ξ)=∫_0 ^ξ ((arctan(ax)−arctan(bx))/x)dx we have ∫_0 ^∞ ((arctan(ax)−arctan(bx))/x)dx =lim_(ξ→+∞) I(ξ) but I(ξ)=∫_0 ^ξ ((arctan(ax))/x)dx−∫_0 ^ξ ((arctan(bx))/x)dx but ∫_0 ^ξ ((arctan(ax))/x) dx=_(ax=t) ∫_0 ^(aξ) ((arctan(t))/(t/a)) (dt/a) =∫_0 ^(aξ) ((arctan(t))/t)dt also ∫_0 ^ξ ((arctan(bx))/x)dx =∫_0 ^(bξ) ((arctan(t))/t)dt ⇒ I(ξ)=∫_0 ^(aξ) ((arctan(t))/t)dt−∫_0 ^(bξ) ((arctan(t))/t)dt =∫_(bξ) ^(aξ) ((arctan(t))/t) dt but ∃ c ∈]bξ,aξ[ / I(ξ)=arctan(ξ)∫_(bξ) ^(aξ) (dt/t) =arctan(ξ)ln(∣(a/b)∣)→(π/2)ln(∣(a/b)∣)(ξ→+∞) ⇒ ∫_0 ^∞ ((arctan(ax)−arctan(bx))/x) dx =(π/2)ln∣(a/b)∣ .](https://www.tinkutara.com/question/Q52541.png)
$$\left.\mathrm{1}\right)\:{let}\:{I}\left(\xi\right)=\int_{\mathrm{0}} ^{\xi} \:\:\:\frac{{arctan}\left({ax}\right)−{arctan}\left({bx}\right)}{{x}}{dx}\:{we}\:{have}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({ax}\right)−{arctan}\left({bx}\right)}{{x}}{dx}\:={lim}_{\xi\rightarrow+\infty} \:{I}\left(\xi\right)\:\:{but} \\ $$$${I}\left(\xi\right)=\int_{\mathrm{0}} ^{\xi} \:\:\frac{{arctan}\left({ax}\right)}{{x}}{dx}−\int_{\mathrm{0}} ^{\xi} \:\frac{{arctan}\left({bx}\right)}{{x}}{dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\xi} \:\:\:\frac{{arctan}\left({ax}\right)}{{x}}\:{dx}=_{{ax}={t}} \:\:\int_{\mathrm{0}} ^{{a}\xi} \:\:\:\frac{{arctan}\left({t}\right)}{\frac{{t}}{{a}}}\:\frac{{dt}}{{a}}\:=\int_{\mathrm{0}} ^{{a}\xi} \:\:\:\frac{{arctan}\left({t}\right)}{{t}}{dt}\:{also} \\ $$$$\int_{\mathrm{0}} ^{\xi} \:\:\:\frac{{arctan}\left({bx}\right)}{{x}}{dx}\:=\int_{\mathrm{0}} ^{{b}\xi} \:\:\frac{{arctan}\left({t}\right)}{{t}}{dt}\:\Rightarrow\:{I}\left(\xi\right)=\int_{\mathrm{0}} ^{{a}\xi} \:\:\frac{{arctan}\left({t}\right)}{{t}}{dt}−\int_{\mathrm{0}} ^{{b}\xi} \:\:\frac{{arctan}\left({t}\right)}{{t}}{dt} \\ $$$$\left.=\int_{{b}\xi} ^{{a}\xi} \:\:\frac{{arctan}\left({t}\right)}{{t}}\:{dt}\:{but}\:\exists\:{c}\:\in\right]{b}\xi,{a}\xi\left[\:/\:{I}\left(\xi\right)={arctan}\left(\xi\right)\int_{{b}\xi} ^{{a}\xi} \:\frac{{dt}}{{t}}\right. \\ $$$$={arctan}\left(\xi\right){ln}\left(\mid\frac{{a}}{{b}}\mid\right)\rightarrow\frac{\pi}{\mathrm{2}}{ln}\left(\mid\frac{{a}}{{b}}\mid\right)\left(\xi\rightarrow+\infty\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({ax}\right)−{arctan}\left({bx}\right)}{{x}}\:{dx}\:=\frac{\pi}{\mathrm{2}}{ln}\mid\frac{{a}}{{b}}\mid\:. \\ $$
Commented by Abdo msup. last updated on 09/Jan/19

$${you}\:{are}\:{welcome}\:.. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19
![1)There is a formula...Frullani intregal... i)if f(x) is continuous function of x for ∞>x≥0 ii)lim_(x→0) f(x)=A lim_(x→∞) f(x)=B then ∫_0 ^∞ ((f(ax)−f(bx))/x)dx=(A−B)ln(b/a) now here f(x)=tan^(−1) (x) lim_(x→0) tan^(−1) x=0←A lim_(x→∞) tan^(−1) (x)=(π/2)←B so ∫_0 ^∞ ((tan^(−1) (ax)−tan^(−1) (bx))/x) [formula(A−B)ln((b/a))] =(0−(π/2))ln((b/a)) =(π/2)ln((a/b))](https://www.tinkutara.com/question/Q52585.png)
$$\left.\mathrm{1}\right){There}\:{is}\:{a}\:{formula}…{Frullani}\:{intregal}… \\ $$$$\left.{i}\right){if}\:{f}\left({x}\right)\:{is}\:{continuous}\:{function}\:{of}\:{x}\:{for}\:\infty>{x}\geqslant\mathrm{0} \\ $$$$\left.{ii}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)={A}\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)={B} \\ $$$${then}\:\int_{\mathrm{0}} ^{\infty} \frac{{f}\left({ax}\right)−{f}\left({bx}\right)}{{x}}{dx}=\left({A}−{B}\right){ln}\frac{{b}}{{a}} \\ $$$${now} \\ $$$${here}\:{f}\left({x}\right)={tan}^{−\mathrm{1}} \left({x}\right)\:\:\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{tan}^{−\mathrm{1}} {x}=\mathrm{0}\leftarrow{A} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{tan}^{−\mathrm{1}} \left({x}\right)=\frac{\pi}{\mathrm{2}}\leftarrow{B} \\ $$$${so}\:\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−\mathrm{1}} \left({ax}\right)−{tan}^{−\mathrm{1}} \left({bx}\right)}{{x}}\:\:\left[{formula}\left({A}−{B}\right){ln}\left(\frac{{b}}{{a}}\right)\right] \\ $$$$=\left(\mathrm{0}−\frac{\pi}{\mathrm{2}}\right){ln}\left(\frac{{b}}{{a}}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(\frac{{a}}{{b}}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19
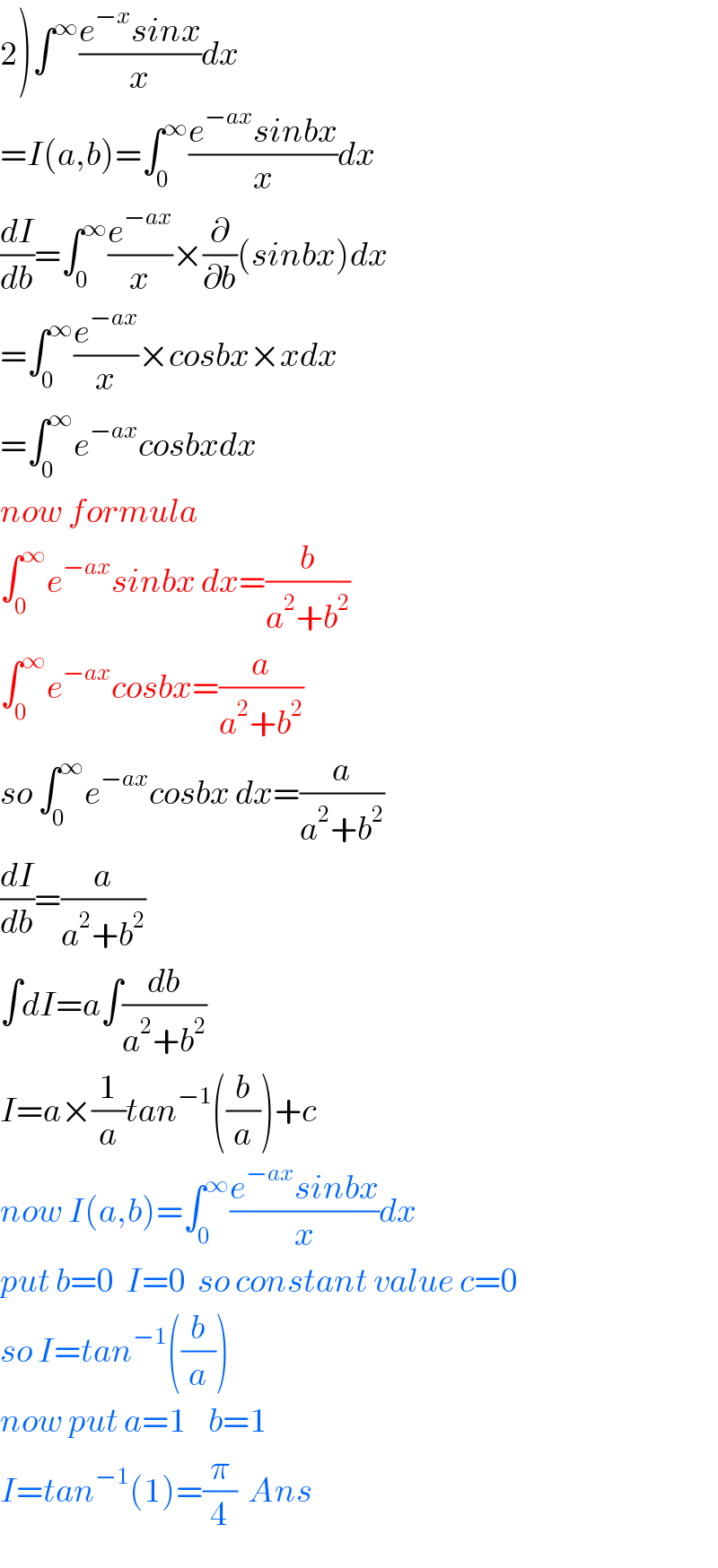
$$\left.\mathrm{2}\right)\int^{\infty} \frac{{e}^{−{x}} {sinx}}{{x}}{dx} \\ $$$$={I}\left({a},{b}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{ax}} {sinbx}}{{x}}{dx} \\ $$$$\frac{{dI}}{{db}}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{ax}} }{{x}}×\frac{\partial}{\partial{b}}\left({sinbx}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{ax}} }{{x}}×{cosbx}×{xdx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} {cosbxdx} \\ $$$${now}\:{formula} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} {sinbx}\:{dx}=\frac{{b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} {cosbx}=\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${so}\:\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} {cosbx}\:{dx}=\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\frac{{dI}}{{db}}=\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\int{dI}={a}\int\frac{{db}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${I}={a}×\frac{\mathrm{1}}{{a}}{tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\right)+{c} \\ $$$${now}\:{I}\left({a},{b}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{ax}} {sinbx}}{{x}}{dx} \\ $$$${put}\:{b}=\mathrm{0}\:\:{I}=\mathrm{0}\:\:{so}\:{constant}\:{value}\:{c}=\mathrm{0} \\ $$$${so}\:{I}={tan}^{−\mathrm{1}} \left(\frac{{b}}{{a}}\right) \\ $$$${now}\:{put}\:{a}=\mathrm{1}\:\:\:\:{b}=\mathrm{1}\:\:\: \\ $$$${I}={tan}^{−\mathrm{1}} \left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}}\:\:{Ans} \\ $$
