Question Number 90759 by M±th+et+s last updated on 25/Apr/20
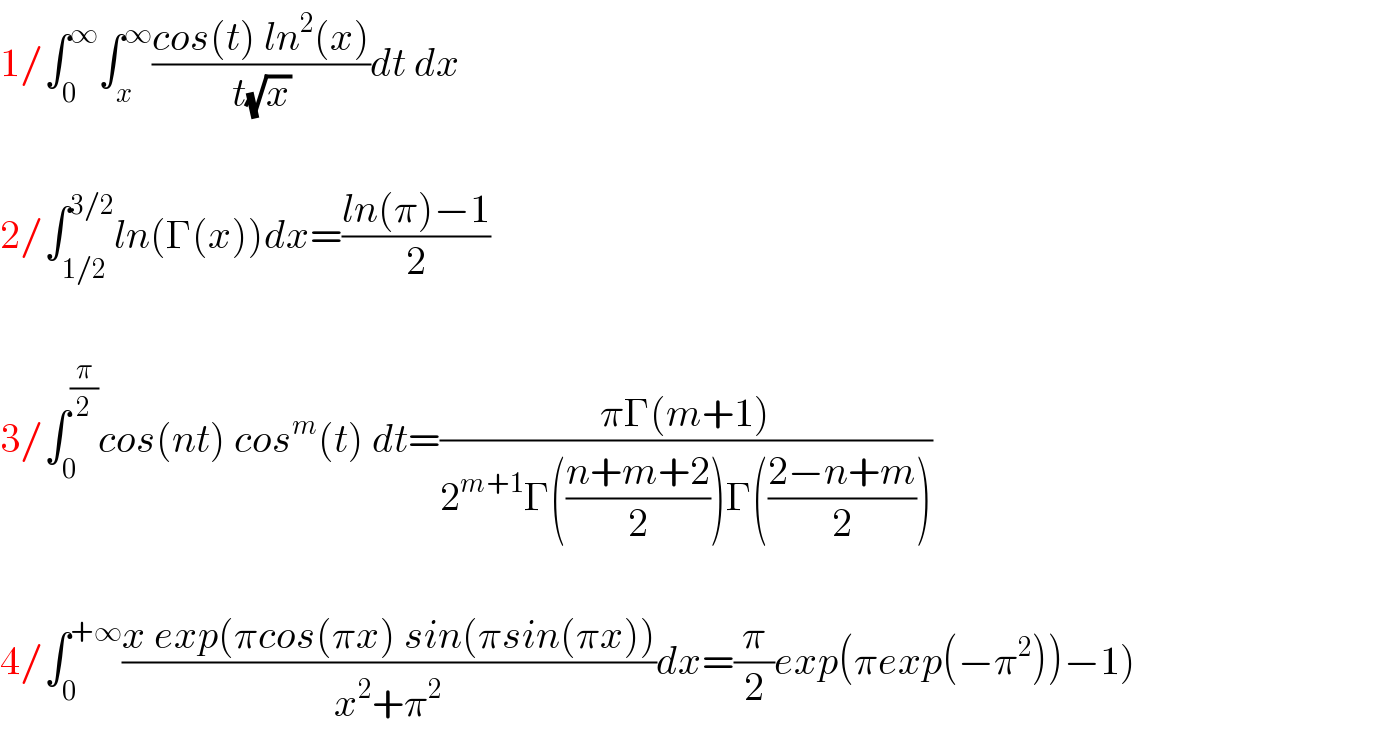
$$\mathrm{1}/\int_{\mathrm{0}} ^{\infty} \int_{{x}} ^{\infty} \frac{{cos}\left({t}\right)\:{ln}^{\mathrm{2}} \left({x}\right)}{{t}\sqrt{{x}}}{dt}\:{dx} \\ $$$$ \\ $$$$\mathrm{2}/\int_{\mathrm{1}/\mathrm{2}} ^{\mathrm{3}/\mathrm{2}} {ln}\left(\Gamma\left({x}\right)\right){dx}=\frac{{ln}\left(\pi\right)−\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{3}/\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left({nt}\right)\:{cos}^{{m}} \left({t}\right)\:{dt}=\frac{\pi\Gamma\left({m}+\mathrm{1}\right)}{\mathrm{2}^{{m}+\mathrm{1}} \Gamma\left(\frac{{n}+{m}+\mathrm{2}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{2}−{n}+{m}}{\mathrm{2}}\right)} \\ $$$$ \\ $$$$\left.\mathrm{4}/\int_{\mathrm{0}} ^{+\infty} \frac{{x}\:{exp}\left(\pi{cos}\left(\pi{x}\right)\:{sin}\left(\pi{sin}\left(\pi{x}\right)\right)\right.}{{x}^{\mathrm{2}} +\pi^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{2}}{exp}\left(\pi{exp}\left(−\pi^{\mathrm{2}} \right)\right)−\mathrm{1}\right) \\ $$
Commented by abdomathmax last updated on 26/Apr/20
![1) let take a try I=∫_0 ^∞ ∫_x ^∞ ((cost ln^2 x)/(t(√x)))dt dx by inversion we get I =∫_0 ^∞ (∫_0 ^t ((ln^2 x)/( (√x))))((cost)/t)dt but ∫_0 ^t ((ln^2 x)/( (√x)))dx =_((√x)=u) ∫_0 ^(√t) ((ln^2 (u^2 ))/u)(2u)du =8 ∫_0 ^(√t) ln^2 u du and by psrts ∫_0 ^(√t) ln^2 u du =[u ln^2 u]_0 ^(√t) −∫_0 ^(√t) u ×((2lnu)/u) du =(√t)ln^2 ((√t))−2 ∫_0 ^(√t) lnu du =(1/4)(√t)ln^2 (t)−2[ulnu−u]_0 ^(√t) =(1/4)(√t)ln^2 (t)−2((√t)ln((√t))−(√t)) =(1/4)(√t)ln^2 (t)−(√t)ln(t)+2(√t) =(1/4)(√t)ln^2 (t)−(√t)ln(t)+2(√t) ⇒ ∫_0 ^t ((ln^2 x)/( (√x)))dx =2(√t)ln^2 (t)−8(√t)ln(t)+16(√t) ⇒ I =∫_0 ^∞ (2(√t)ln^2 (t)−8(√t)ln(t)+16(√t))((cost)/t)dt =_((√t)=z) ∫_0 ^∞ (2zln^2 (z^2 )−8zln(z^2 )+16z)((cos(z^2 ))/z^2 )(2z)dz =∫_0 ^∞ (4ln^2 (z^2 )−16ln(z^2 )+32)cos(z^2 )dz =8∫_0 ^∞ ln^2 (z)cos(z^2 )dz−32 ∫_0 ^∞ ln(z)cos(z^2 )dz +32 ∫_0 ^∞ cos(z^2 )dz ∫_0 ^∞ cos(z^2 )dz =Re(∫_0 ^∞ e^(−iz^2 ) dz) ∫_0 ^∞ e^(−iz^2 ) dz =∫_0 ^∞ e^(−((√i)z)^2 ) dz =_((√i)z =u) ∫_0 ^∞ e^(−u^2 ) (du/( (√i))) =(1/e^((iπ)/4) ) ×((√π)/2) =((√π)/2)((1/( (√2)))−(i/( (√2)))) ⇒∫_0 ^∞ cos(z^2 )dz =((√π)/(2(√2))) ...be continuesd...](https://www.tinkutara.com/question/Q90782.png)
$$\left.\mathrm{1}\right)\:{let}\:{take}\:{a}\:{try}\:\:{I}=\int_{\mathrm{0}} ^{\infty} \int_{{x}} ^{\infty} \:\frac{{cost}\:{ln}^{\mathrm{2}} {x}}{{t}\sqrt{{x}}}{dt}\:{dx}\:{by}\:{inversion} \\ $$$${we}\:{get}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{0}} ^{{t}} \:\frac{{ln}^{\mathrm{2}} {x}}{\:\sqrt{{x}}}\right)\frac{{cost}}{{t}}{dt}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{{t}} \:\frac{{ln}^{\mathrm{2}} {x}}{\:\sqrt{{x}}}{dx}\:=_{\sqrt{{x}}={u}} \:\:\:\int_{\mathrm{0}} ^{\sqrt{{t}}} \:\frac{{ln}^{\mathrm{2}} \left({u}^{\mathrm{2}} \right)}{{u}}\left(\mathrm{2}{u}\right){du} \\ $$$$=\mathrm{8}\:\int_{\mathrm{0}} ^{\sqrt{{t}}} {ln}^{\mathrm{2}} {u}\:{du}\:\:\:{and}\:{by}\:{psrts} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{{t}}} \:{ln}^{\mathrm{2}} {u}\:{du}\:=\left[{u}\:{ln}^{\mathrm{2}} {u}\right]_{\mathrm{0}} ^{\sqrt{{t}}} −\int_{\mathrm{0}} ^{\sqrt{{t}}} {u}\:×\frac{\mathrm{2}{lnu}}{{u}}\:{du} \\ $$$$=\sqrt{{t}}{ln}^{\mathrm{2}} \left(\sqrt{{t}}\right)−\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{{t}}} \:{lnu}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{{t}}{ln}^{\mathrm{2}} \left({t}\right)−\mathrm{2}\left[{ulnu}−{u}\right]_{\mathrm{0}} ^{\sqrt{{t}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{{t}}{ln}^{\mathrm{2}} \left({t}\right)−\mathrm{2}\left(\sqrt{{t}}{ln}\left(\sqrt{{t}}\right)−\sqrt{{t}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{{t}}{ln}^{\mathrm{2}} \left({t}\right)−\sqrt{{t}}{ln}\left({t}\right)+\mathrm{2}\sqrt{{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{{t}}{ln}^{\mathrm{2}} \left({t}\right)−\sqrt{{t}}{ln}\left({t}\right)+\mathrm{2}\sqrt{{t}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{{t}} \:\frac{{ln}^{\mathrm{2}} {x}}{\:\sqrt{{x}}}{dx}\:=\mathrm{2}\sqrt{{t}}{ln}^{\mathrm{2}} \left({t}\right)−\mathrm{8}\sqrt{{t}}{ln}\left({t}\right)+\mathrm{16}\sqrt{{t}}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{2}\sqrt{{t}}{ln}^{\mathrm{2}} \left({t}\right)−\mathrm{8}\sqrt{{t}}{ln}\left({t}\right)+\mathrm{16}\sqrt{{t}}\right)\frac{{cost}}{{t}}{dt} \\ $$$$=_{\sqrt{{t}}={z}} \:\:\int_{\mathrm{0}} ^{\infty} \left(\mathrm{2}{zln}^{\mathrm{2}} \left({z}^{\mathrm{2}} \right)−\mathrm{8}{zln}\left({z}^{\mathrm{2}} \right)+\mathrm{16}{z}\right)\frac{{cos}\left({z}^{\mathrm{2}} \right)}{{z}^{\mathrm{2}} }\left(\mathrm{2}{z}\right){dz} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{4}{ln}^{\mathrm{2}} \left({z}^{\mathrm{2}} \right)−\mathrm{16}{ln}\left({z}^{\mathrm{2}} \right)+\mathrm{32}\right){cos}\left({z}^{\mathrm{2}} \right){dz} \\ $$$$=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \:{ln}^{\mathrm{2}} \left({z}\right){cos}\left({z}^{\mathrm{2}} \right){dz}−\mathrm{32}\:\int_{\mathrm{0}} ^{\infty} \:{ln}\left({z}\right){cos}\left({z}^{\mathrm{2}} \right){dz} \\ $$$$+\mathrm{32}\:\int_{\mathrm{0}} ^{\infty} \:{cos}\left({z}^{\mathrm{2}} \right){dz} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{cos}\left({z}^{\mathrm{2}} \right){dz}\:={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{iz}^{\mathrm{2}} } {dz}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{iz}^{\mathrm{2}} } {dz}\:=\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\sqrt{{i}}{z}\right)^{\mathrm{2}} } {dz} \\ $$$$=_{\sqrt{{i}}{z}\:={u}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{u}^{\mathrm{2}} } \:\frac{{du}}{\:\sqrt{{i}}}\:\:=\frac{\mathrm{1}}{{e}^{\frac{{i}\pi}{\mathrm{4}}} }\:×\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{cos}\left({z}^{\mathrm{2}} \right){dz}\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$…{be}\:{continuesd}… \\ $$
