Question Number 61625 by Sharath Kumar last updated on 05/Jun/19
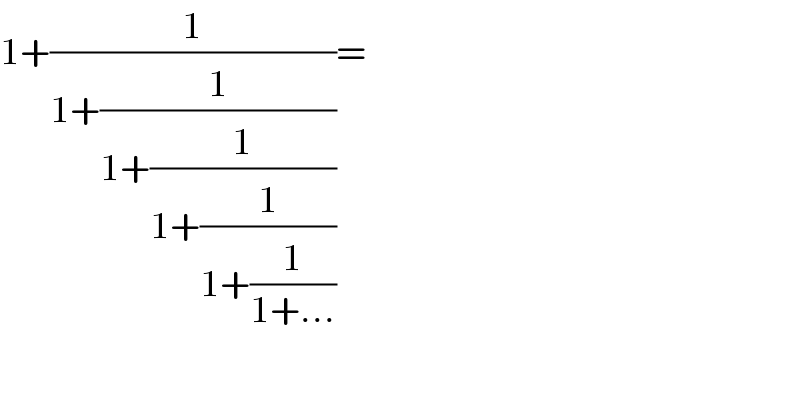
$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+…}}}}}= \\ $$
Answered by MJS last updated on 05/Jun/19

$${x}=\mathrm{1}+\frac{\mathrm{1}}{{x}}\:\wedge\:{x}>\mathrm{1}\:\Rightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by Kunal12588 last updated on 05/Jun/19
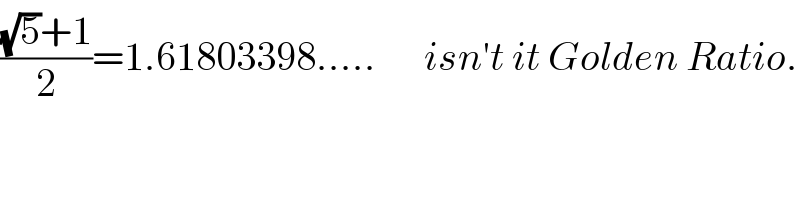
$$\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}=\mathrm{1}.\mathrm{61803398}…..\:\:\:\:\:\:{isn}'{t}\:{it}\:{Golden}\:{Ratio}. \\ $$
Commented by MJS last updated on 06/Jun/19

$$\mathrm{yes} \\ $$
