1-1-1-1-1-1-i-i-i-2-1-where-is-the-mistake-

Question Number 171406 by floor(10²Eta[1]) last updated on 14/Jun/22

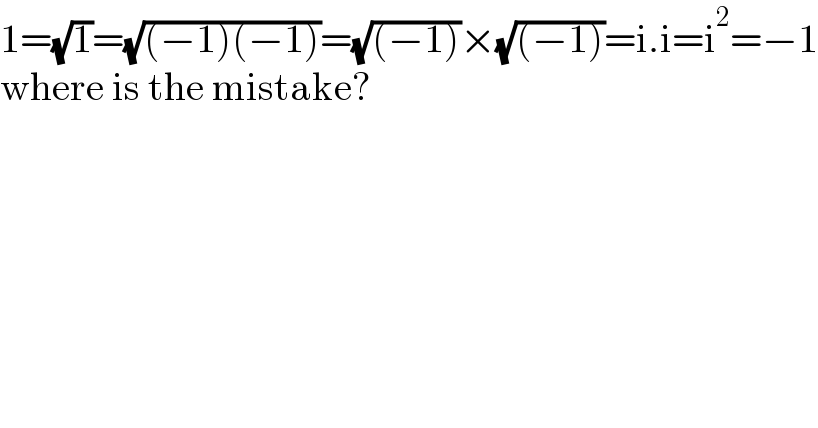
$$\mathrm{1}=\sqrt{\mathrm{1}}=\sqrt{\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)}=\sqrt{\left(−\mathrm{1}\right)}×\sqrt{\left(−\mathrm{1}\right)}=\mathrm{i}.\mathrm{i}=\mathrm{i}^{\mathrm{2}} =−\mathrm{1} \\ $$$$\mathrm{where}\:\mathrm{is}\:\mathrm{the}\:\mathrm{mistake}? \\ $$

Commented by infinityaction last updated on 14/Jun/22

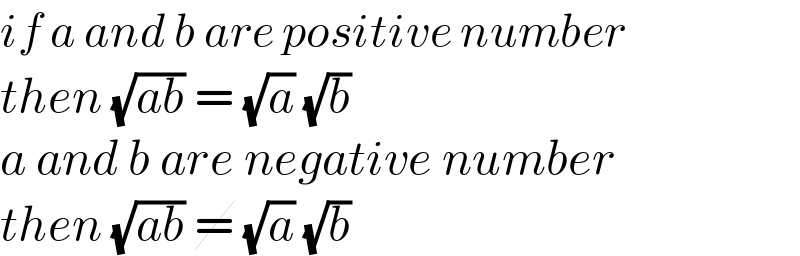
if a and b are positive number then (√(ab)) = (√a) (√b) a and b are negative number then (√(ab)) = (√a) (√b)

$${if}\:{a}\:{and}\:{b}\:{are}\:{positive}\:{number} \\ $$$${then}\:\sqrt{{ab}}\:=\:\sqrt{{a}}\:\sqrt{{b}} \\ $$$${a}\:{and}\:{b}\:{are}\:{negative}\:{number} \\ $$$${then}\:\sqrt{{ab}}\:\cancel{=}\:\sqrt{{a}}\:\sqrt{{b}} \\ $$

Answered by MJS_new last updated on 14/Jun/22

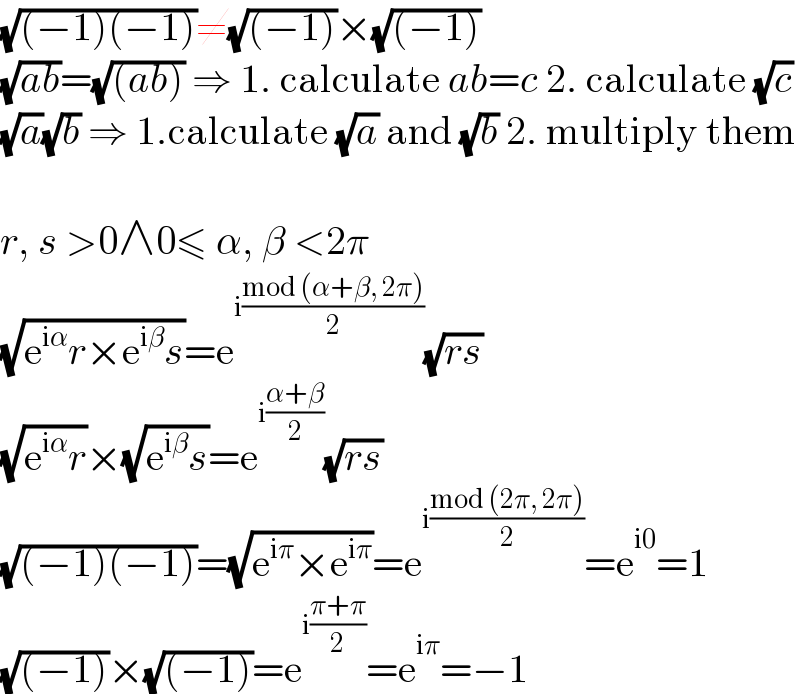
(√((−1)(−1)))≠(√((−1)))×(√((−1))) (√(ab))=(√((ab))) ⇒ 1. calculate ab=c 2. calculate (√c) (√a)(√b) ⇒ 1.calculate (√a) and (√b) 2. multiply them r, s >0∧0≤ α, β <2π (√(e^(iα) r×e^(iβ) s))=e^(i((mod (α+β, 2π))/2)) (√(rs)) (√(e^(iα) r))×(√(e^(iβ) s))=e^(i((α+β)/2)) (√(rs)) (√((−1)(−1)))=(√(e^(iπ) ×e^(iπ) ))=e^(i((mod (2π, 2π))/2)) =e^(i0) =1 (√((−1)))×(√((−1)))=e^(i((π+π)/2)) =e^(iπ) =−1

$$\sqrt{\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)}\neq\sqrt{\left(−\mathrm{1}\right)}×\sqrt{\left(−\mathrm{1}\right)} \\ $$$$\sqrt{{ab}}=\sqrt{\left({ab}\right)}\:\Rightarrow\:\mathrm{1}.\:\mathrm{calculate}\:{ab}={c}\:\mathrm{2}.\:\mathrm{calculate}\:\sqrt{{c}} \\ $$$$\sqrt{{a}}\sqrt{{b}}\:\Rightarrow\:\mathrm{1}.\mathrm{calculate}\:\sqrt{{a}}\:\mathrm{and}\:\sqrt{{b}}\:\mathrm{2}.\:\mathrm{multiply}\:\mathrm{them} \\ $$$$ \\ $$$${r},\:{s}\:>\mathrm{0}\wedge\mathrm{0}\leqslant\:\alpha,\:\beta\:<\mathrm{2}\pi \\ $$$$\sqrt{\mathrm{e}^{\mathrm{i}\alpha} {r}×\mathrm{e}^{\mathrm{i}\beta} {s}}=\mathrm{e}^{\mathrm{i}\frac{\mathrm{mod}\:\left(\alpha+\beta,\:\mathrm{2}\pi\right)}{\mathrm{2}}} \sqrt{{rs}} \\ $$$$\sqrt{\mathrm{e}^{\mathrm{i}\alpha} {r}}×\sqrt{\mathrm{e}^{\mathrm{i}\beta} {s}}=\mathrm{e}^{\mathrm{i}\frac{\alpha+\beta}{\mathrm{2}}} \sqrt{{rs}} \\ $$$$\sqrt{\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)}=\sqrt{\mathrm{e}^{\mathrm{i}\pi} ×\mathrm{e}^{\mathrm{i}\pi} }=\mathrm{e}^{\mathrm{i}\frac{\mathrm{mod}\:\left(\mathrm{2}\pi,\:\mathrm{2}\pi\right)}{\mathrm{2}}} =\mathrm{e}^{\mathrm{i0}} =\mathrm{1} \\ $$$$\sqrt{\left(−\mathrm{1}\right)}×\sqrt{\left(−\mathrm{1}\right)}=\mathrm{e}^{\mathrm{i}\frac{\pi+\pi}{\mathrm{2}}} =\mathrm{e}^{\mathrm{i}\pi} =−\mathrm{1} \\ $$

Facebook Tweet Pin

1-1-1-1-1-1-i-i-i-2-1-where-is-the-mistake-

Leave a Reply Cancel reply