Menu Close

1-1-1-2-1-3-1-2018-

Tinku Tara 0 Comments
Pin




Question Number 40378 by S.HER last updated on 21/Jul/18
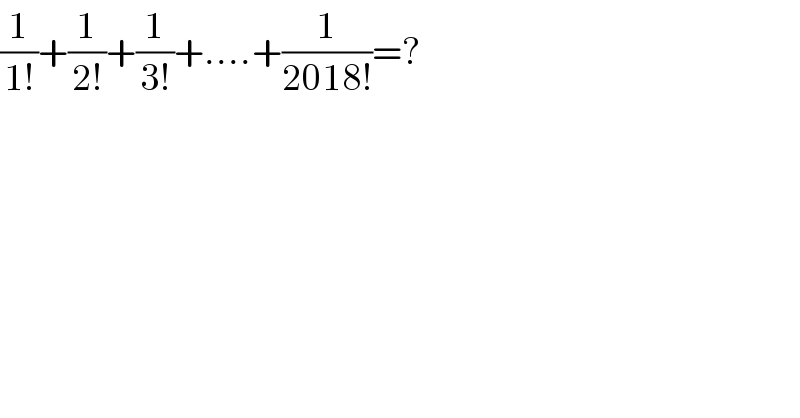
(1/(1!))+(1/(2!))+(1/(3!))+....+(1/(2018!))=?
$$\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+….+\frac{\mathrm{1}}{\mathrm{2018}!}=? \\ $$
Commented by maxmathsup by imad last updated on 21/Jul/18
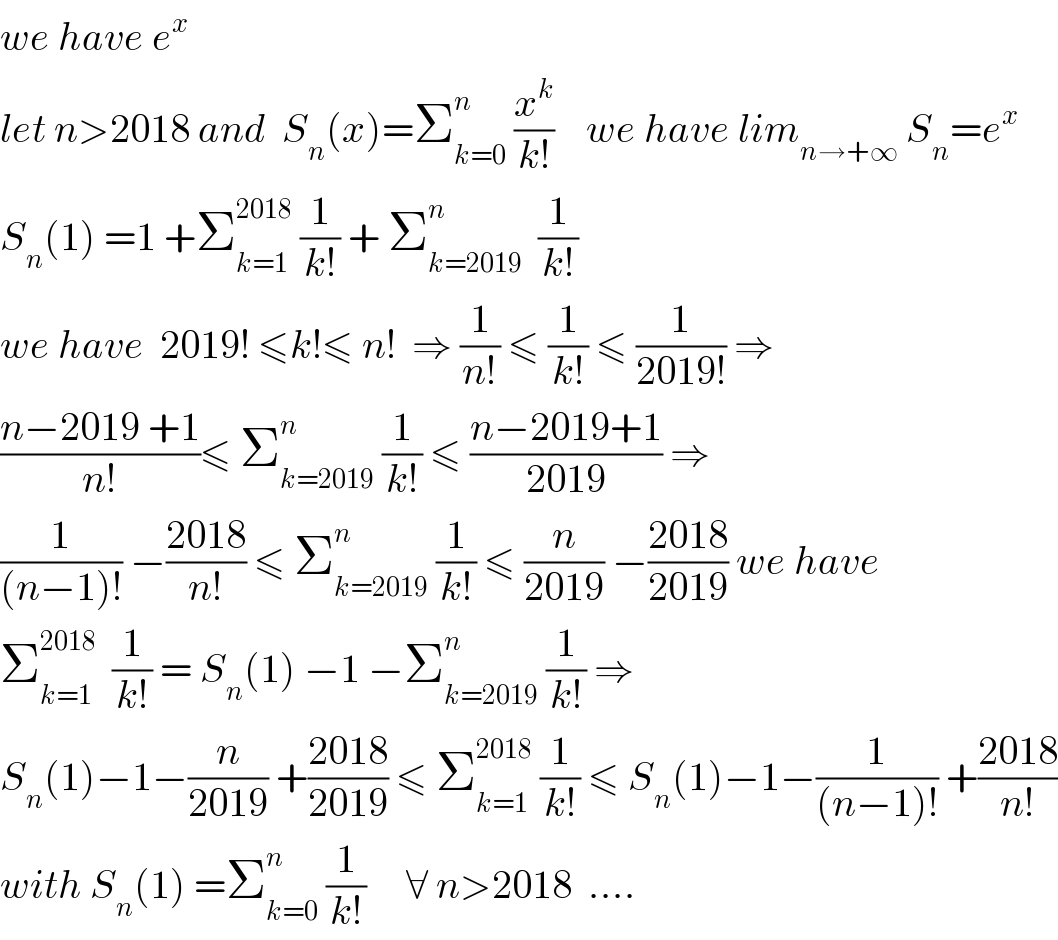
we have e^x let n>2018 and S_n (x)=Σ_(k=0) ^n (x^k /(k!)) we have lim_(n→+∞) S_n =e^x S_n (1) =1 +Σ_(k=1) ^(2018) (1/(k!)) + Σ_(k=2019) ^n (1/(k!)) we have 2019! ≤k!≤ n! ⇒ (1/(n!)) ≤ (1/(k!)) ≤ (1/(2019!)) ⇒ ((n−2019 +1)/(n!))≤ Σ_(k=2019) ^n (1/(k!)) ≤ ((n−2019+1)/(2019)) ⇒ (1/((n−1)!)) −((2018)/(n!)) ≤ Σ_(k=2019) ^n (1/(k!)) ≤ (n/(2019)) −((2018)/(2019)) we have Σ_(k=1) ^(2018) (1/(k!)) = S_n (1) −1 −Σ_(k=2019) ^n (1/(k!)) ⇒ S_n (1)−1−(n/(2019)) +((2018)/(2019)) ≤ Σ_(k=1) ^(2018) (1/(k!)) ≤ S_n (1)−1−(1/((n−1)!)) +((2018)/(n!)) with S_n (1) =Σ_(k=0) ^n (1/(k!)) ∀ n>2018 ....
$${we}\:{have}\:{e}^{{x}} \: \\ $$$${let}\:{n}>\mathrm{2018}\:{and}\:\:{S}_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{{x}^{{k}} }{{k}!}\:\:\:\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} ={e}^{{x}} \\ $$$${S}_{{n}} \left(\mathrm{1}\right)\:=\mathrm{1}\:+\sum_{{k}=\mathrm{1}} ^{\mathrm{2018}} \:\frac{\mathrm{1}}{{k}!}\:+\:\sum_{{k}=\mathrm{2019}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}!} \\ $$$${we}\:{have}\:\:\mathrm{2019}!\:\leqslant{k}!\leqslant\:{n}!\:\:\Rightarrow\:\frac{\mathrm{1}}{{n}!}\:\leqslant\:\frac{\mathrm{1}}{{k}!}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{2019}!}\:\Rightarrow \\ $$$$\frac{{n}−\mathrm{2019}\:+\mathrm{1}}{{n}!}\leqslant\:\sum_{{k}=\mathrm{2019}} ^{{n}} \:\frac{\mathrm{1}}{{k}!}\:\leqslant\:\frac{{n}−\mathrm{2019}+\mathrm{1}}{\mathrm{2019}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\:−\frac{\mathrm{2018}}{{n}!}\:\leqslant\:\sum_{{k}=\mathrm{2019}} ^{{n}} \:\frac{\mathrm{1}}{{k}!}\:\leqslant\:\frac{{n}}{\mathrm{2019}}\:−\frac{\mathrm{2018}}{\mathrm{2019}}\:{we}\:{have} \\ $$$$\sum_{{k}=\mathrm{1}} ^{\mathrm{2018}} \:\:\frac{\mathrm{1}}{{k}!}\:=\:{S}_{{n}} \left(\mathrm{1}\right)\:−\mathrm{1}\:−\sum_{{k}=\mathrm{2019}} ^{{n}} \:\frac{\mathrm{1}}{{k}!}\:\Rightarrow \\ $$$${S}_{{n}} \left(\mathrm{1}\right)−\mathrm{1}−\frac{{n}}{\mathrm{2019}}\:+\frac{\mathrm{2018}}{\mathrm{2019}}\:\leqslant\:\sum_{{k}=\mathrm{1}} ^{\mathrm{2018}} \:\frac{\mathrm{1}}{{k}!}\:\leqslant\:{S}_{{n}} \left(\mathrm{1}\right)−\mathrm{1}−\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\:+\frac{\mathrm{2018}}{{n}!} \\ $$$${with}\:{S}_{{n}} \left(\mathrm{1}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{k}!}\:\:\:\:\:\forall\:{n}>\mathrm{2018}\:\:…. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jul/18
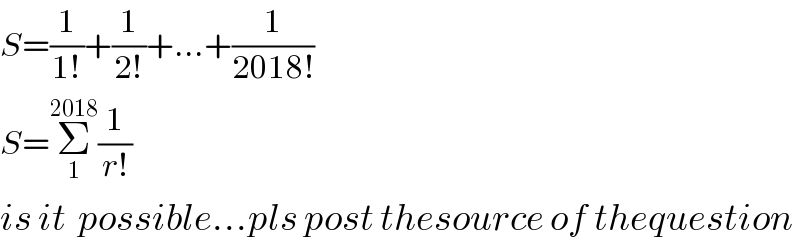
S=(1/(1!))+(1/(2!))+...+(1/(2018!)) S=Σ_1 ^(2018) (1/(r!)) is it possible...pls post thesource of thequestion
$${S}=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+…+\frac{\mathrm{1}}{\mathrm{2018}!} \\ $$$${S}=\underset{\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}\frac{\mathrm{1}}{{r}!} \\ $$$${is}\:{it}\:\:{possible}…{pls}\:{post}\:{thesource}\:{of}\:{thequestion} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jul/18
Answered by MJS last updated on 21/Jul/18
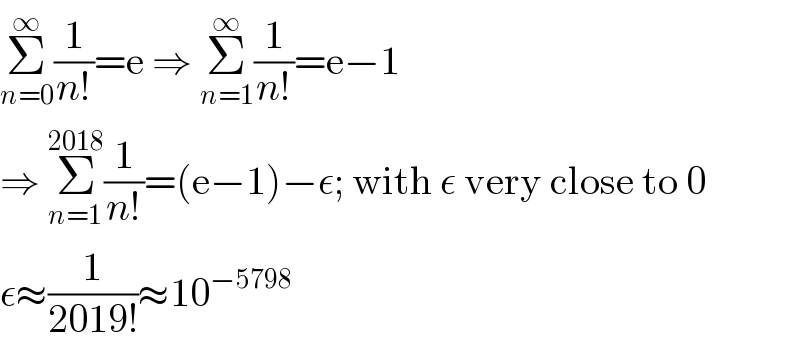
Σ_(n=0) ^∞ (1/(n!))=e ⇒ Σ_(n=1) ^∞ (1/(n!))=e−1 ⇒ Σ_(n=1) ^(2018) (1/(n!))=(e−1)−ε; with ε very close to 0 ε≈(1/(2019!))≈10^(−5798)
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}=\mathrm{e}\:\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}=\mathrm{e}−\mathrm{1} \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}\frac{\mathrm{1}}{{n}!}=\left(\mathrm{e}−\mathrm{1}\right)−\epsilon;\:\mathrm{with}\:\epsilon\:\mathrm{very}\:\mathrm{close}\:\mathrm{to}\:\mathrm{0} \\ $$$$\epsilon\approx\frac{\mathrm{1}}{\mathrm{2019}!}\approx\mathrm{10}^{−\mathrm{5798}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jul/18
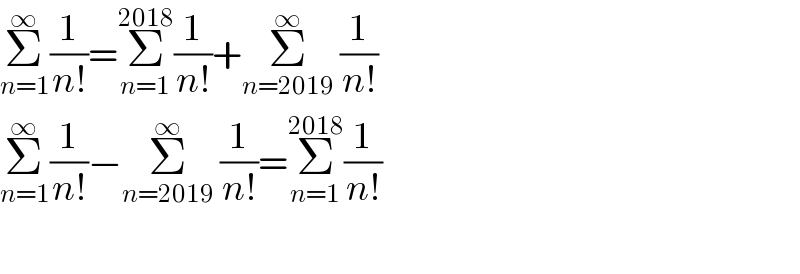
Σ_(n=1) ^∞ (1/(n!))=Σ_(n=1) ^(2018) (1/(n!))+Σ_(n=2019) ^∞ (1/(n!)) Σ_(n=1) ^∞ (1/(n!))−Σ_(n=2019) ^∞ (1/(n!))=Σ_(n=1) ^(2018) (1/(n!))
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}\frac{\mathrm{1}}{{n}!}+\underset{{n}=\mathrm{2019}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}!} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}−\underset{{n}=\mathrm{2019}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}!}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2018}} {\sum}}\frac{\mathrm{1}}{{n}!} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *