Question Number 90251 by Hanumantha Rao DAMARAJU last updated on 22/Apr/20
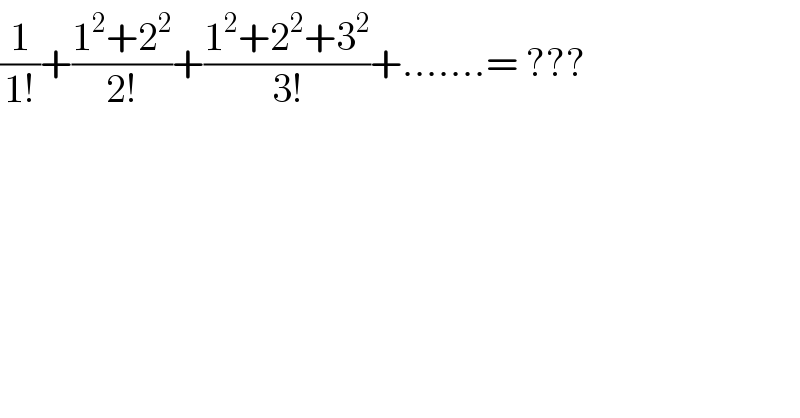
$$\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }{\mathrm{3}!}+…….=\:??? \\ $$
Commented by MJS last updated on 22/Apr/20
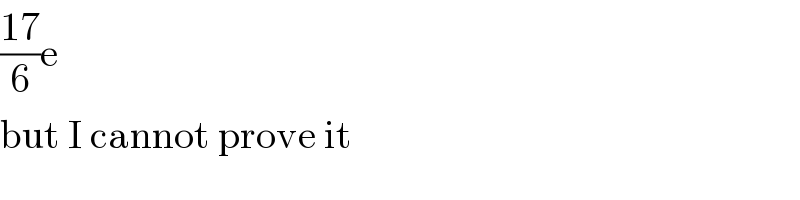
$$\frac{\mathrm{17}}{\mathrm{6}}\mathrm{e} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{cannot}\:\mathrm{prove}\:\mathrm{it} \\ $$
Commented by mathmax by abdo last updated on 22/Apr/20
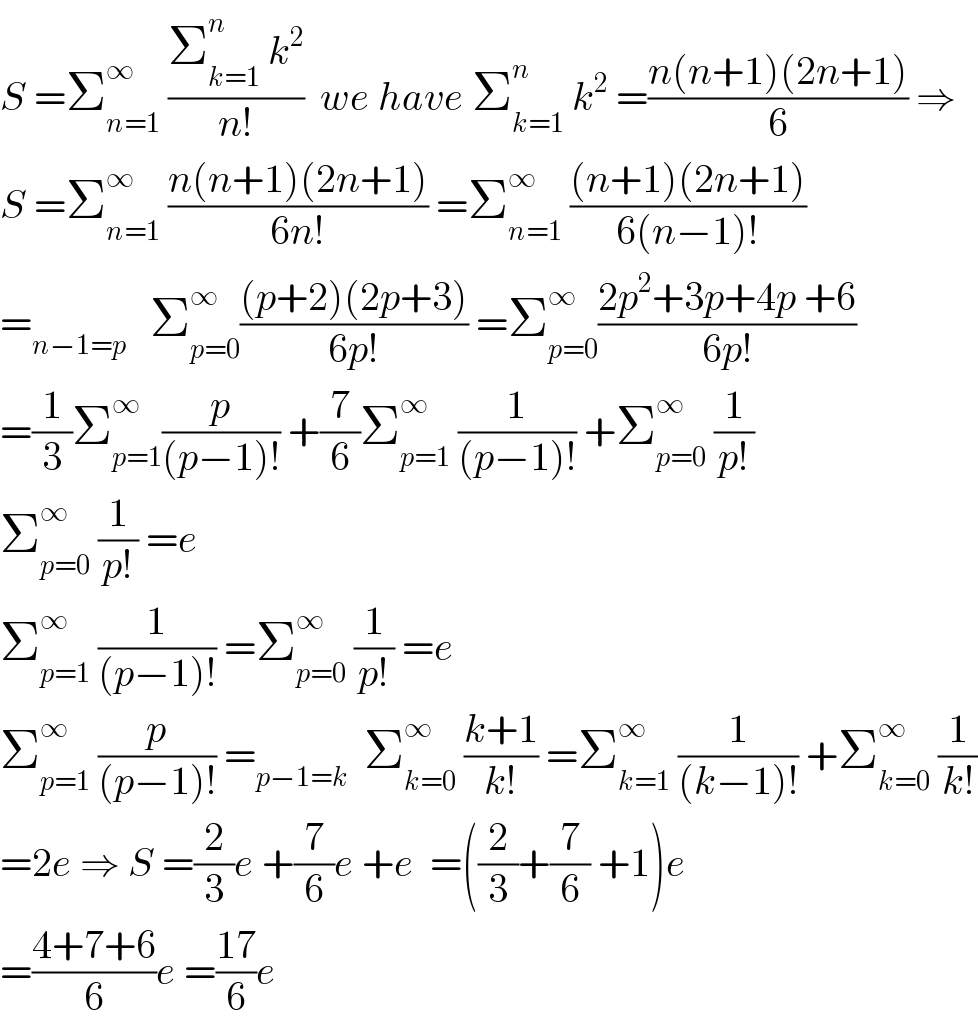
$${S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}} }{{n}!}\:\:{we}\:{have}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}} \:=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\:\Rightarrow \\ $$$${S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}{n}!}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}\left({n}−\mathrm{1}\right)!} \\ $$$$=_{{n}−\mathrm{1}={p}} \:\:\:\sum_{{p}=\mathrm{0}} ^{\infty} \frac{\left({p}+\mathrm{2}\right)\left(\mathrm{2}{p}+\mathrm{3}\right)}{\mathrm{6}{p}!}\:=\sum_{{p}=\mathrm{0}} ^{\infty} \frac{\mathrm{2}{p}^{\mathrm{2}} +\mathrm{3}{p}+\mathrm{4}{p}\:+\mathrm{6}}{\mathrm{6}{p}!} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\sum_{{p}=\mathrm{1}} ^{\infty} \frac{{p}}{\left({p}−\mathrm{1}\right)!}\:+\frac{\mathrm{7}}{\mathrm{6}}\sum_{{p}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left({p}−\mathrm{1}\right)!}\:+\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{p}!} \\ $$$$\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{p}!}\:={e} \\ $$$$\sum_{{p}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left({p}−\mathrm{1}\right)!}\:=\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{p}!}\:={e} \\ $$$$\sum_{{p}=\mathrm{1}} ^{\infty} \:\frac{{p}}{\left({p}−\mathrm{1}\right)!}\:=_{{p}−\mathrm{1}={k}} \:\:\sum_{{k}=\mathrm{0}} ^{\infty} \:\frac{{k}+\mathrm{1}}{{k}!}\:=\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!}\:+\sum_{{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{k}!} \\ $$$$=\mathrm{2}{e}\:\Rightarrow\:{S}\:=\frac{\mathrm{2}}{\mathrm{3}}{e}\:+\frac{\mathrm{7}}{\mathrm{6}}{e}\:+{e}\:\:=\left(\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{7}}{\mathrm{6}}\:+\mathrm{1}\right){e} \\ $$$$=\frac{\mathrm{4}+\mathrm{7}+\mathrm{6}}{\mathrm{6}}{e}\:=\frac{\mathrm{17}}{\mathrm{6}}{e} \\ $$
Answered by TANMAY PANACEA. last updated on 22/Apr/20
![T_r =((1^2 +2^2 +3^2 +..+r^2 )/(r!))=((r(r+1)(2r+1))/(6r!)) T_r =(1/6)[(((r+1)(2r+1))/((r−1)!))]=(1/6)[((2r^2 +3r+1)/((r−1)!))] =(1/6)[((2(r−1)^2 +7r−7+6)/((r−1)!))] =(1/6)[((2(r−1))/((r−2)!))+(7/((r−2)!))+(6/((r−1)!))] =(1/6)[((2r−4+2)/((r−2)!))+(7/((r−2)!))+(6/((r−1)!))] =(1/6)[(2/((r−3)!))+(9/((r−2)!))+(6/((r−1)!))] T_4 =(1/6)[(2/(1!))+(9/(2!))+(6/(3!))] T_5 =(1/6)[(2/(2!))+(9/(3!))+(6/(4!))] T_6 =(1/6)[(2/(3!))+(9/(4!))+(6/(5!))] ... ... T_r =(1/6)[(2/((r−3)!))+(9/((r−2)!))+(6/((r−1)!))] ... ... add them S=Σ_(r=4) ^∞ T_r =(1/6)[2×e+9(e−(1/(1!)))+6(e−(1/(1!))−(1/(2!)))] =(1/6)[17e−9−6−3]=((17e)/6)−((18)/6) hence required answer is T_1 +T_2 +T_3 +Σ_(r=4) ^∞ T_r =(1/(1!))+((1^2 +2^2 )/(2!))+((1^2 +2^2 +3^2 )/(3!))+((17e)/6)−3 =1+(5/2)+((14)/6)−3+((17e)/6) =((6+15+14−18)/6)+((17e)/6) =((17)/6)+((17)/6)e=((17)/6)(1+e) pls check](https://www.tinkutara.com/question/Q90290.png)
$${T}_{{r}} =\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +..+{r}^{\mathrm{2}} }{{r}!}=\frac{{r}\left({r}+\mathrm{1}\right)\left(\mathrm{2}{r}+\mathrm{1}\right)}{\mathrm{6}{r}!} \\ $$$${T}_{{r}} =\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\left({r}+\mathrm{1}\right)\left(\mathrm{2}{r}+\mathrm{1}\right)}{\left({r}−\mathrm{1}\right)!}\right]=\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\mathrm{2}{r}^{\mathrm{2}} +\mathrm{3}{r}+\mathrm{1}}{\left({r}−\mathrm{1}\right)!}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\mathrm{2}\left({r}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{7}{r}−\mathrm{7}+\mathrm{6}}{\left({r}−\mathrm{1}\right)!}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\mathrm{2}\left({r}−\mathrm{1}\right)}{\left({r}−\mathrm{2}\right)!}+\frac{\mathrm{7}}{\left({r}−\mathrm{2}\right)!}+\frac{\mathrm{6}}{\left({r}−\mathrm{1}\right)!}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\mathrm{2}{r}−\mathrm{4}+\mathrm{2}}{\left({r}−\mathrm{2}\right)!}+\frac{\mathrm{7}}{\left({r}−\mathrm{2}\right)!}+\frac{\mathrm{6}}{\left({r}−\mathrm{1}\right)!}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\mathrm{2}}{\left({r}−\mathrm{3}\right)!}+\frac{\mathrm{9}}{\left({r}−\mathrm{2}\right)!}+\frac{\mathrm{6}}{\left({r}−\mathrm{1}\right)!}\right] \\ $$$${T}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{9}}{\mathrm{2}!}+\frac{\mathrm{6}}{\mathrm{3}!}\right] \\ $$$${T}_{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\mathrm{2}}{\mathrm{2}!}+\frac{\mathrm{9}}{\mathrm{3}!}+\frac{\mathrm{6}}{\mathrm{4}!}\right] \\ $$$${T}_{\mathrm{6}} =\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\mathrm{2}}{\mathrm{3}!}+\frac{\mathrm{9}}{\mathrm{4}!}+\frac{\mathrm{6}}{\mathrm{5}!}\right] \\ $$$$… \\ $$$$… \\ $$$${T}_{{r}} =\frac{\mathrm{1}}{\mathrm{6}}\left[\frac{\mathrm{2}}{\left({r}−\mathrm{3}\right)!}+\frac{\mathrm{9}}{\left({r}−\mathrm{2}\right)!}+\frac{\mathrm{6}}{\left({r}−\mathrm{1}\right)!}\right] \\ $$$$… \\ $$$$… \\ $$$${add}\:{them} \\ $$$${S}=\underset{{r}=\mathrm{4}} {\overset{\infty} {\sum}}{T}_{{r}} \:=\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{2}×{e}+\mathrm{9}\left({e}−\frac{\mathrm{1}}{\mathrm{1}!}\right)+\mathrm{6}\left({e}−\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{1}}{\mathrm{2}!}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{17}{e}−\mathrm{9}−\mathrm{6}−\mathrm{3}\right]=\frac{\mathrm{17}\boldsymbol{{e}}}{\mathrm{6}}−\frac{\mathrm{18}}{\mathrm{6}} \\ $$$$\boldsymbol{{hence}}\:\boldsymbol{{required}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{T}}_{\mathrm{1}} +{T}_{\mathrm{2}} +{T}_{\mathrm{3}} +\underset{{r}=\mathrm{4}} {\overset{\infty} {\sum}}{T}_{{r}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }{\mathrm{3}!}+\frac{\mathrm{17}\boldsymbol{{e}}}{\mathrm{6}}−\mathrm{3} \\ $$$$=\mathrm{1}+\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{14}}{\mathrm{6}}−\mathrm{3}+\frac{\mathrm{17}\boldsymbol{{e}}}{\mathrm{6}} \\ $$$$=\frac{\mathrm{6}+\mathrm{15}+\mathrm{14}−\mathrm{18}}{\mathrm{6}}+\frac{\mathrm{17}\boldsymbol{{e}}}{\mathrm{6}} \\ $$$$=\frac{\mathrm{17}}{\mathrm{6}}+\frac{\mathrm{17}}{\mathrm{6}}\boldsymbol{{e}}=\frac{\mathrm{17}}{\mathrm{6}}\left(\mathrm{1}+\boldsymbol{{e}}\right) \\ $$$$\boldsymbol{{pls}}\:\boldsymbol{{check}} \\ $$
Commented by mathmax by abdo last updated on 22/Apr/20
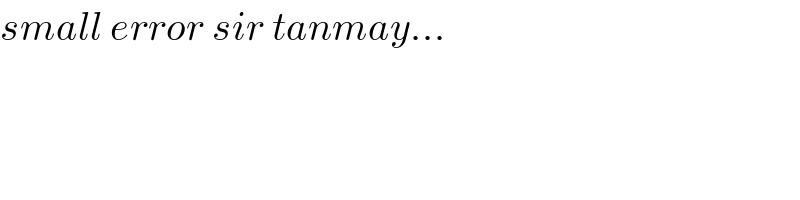
$${small}\:{error}\:{sir}\:{tanmay}… \\ $$
