Question Number 126934 by Dwaipayan Shikari last updated on 25/Dec/20
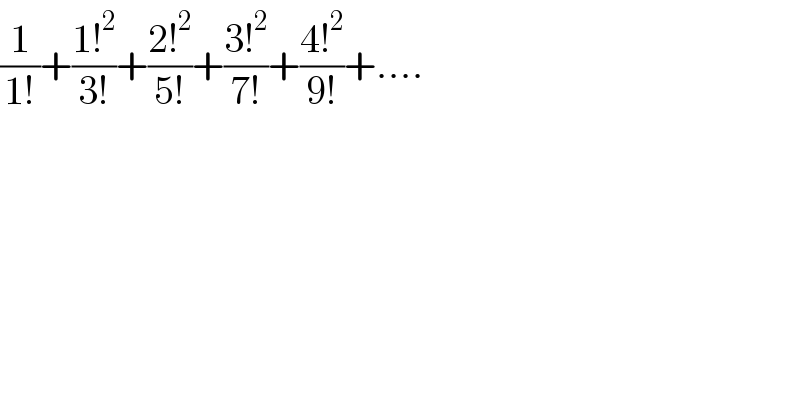
$$\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}!^{\mathrm{2}} }{\mathrm{3}!}+\frac{\mathrm{2}!^{\mathrm{2}} }{\mathrm{5}!}+\frac{\mathrm{3}!^{\mathrm{2}} }{\mathrm{7}!}+\frac{\mathrm{4}!^{\mathrm{2}} }{\mathrm{9}!}+…. \\ $$
Commented by Dwaipayan Shikari last updated on 25/Dec/20
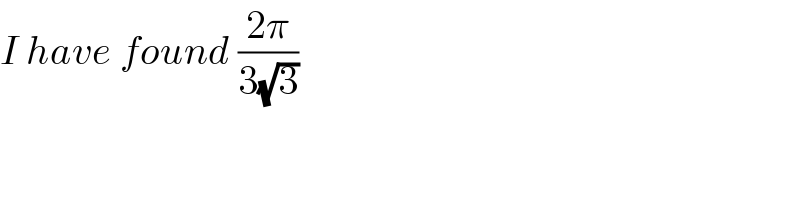
$${I}\:{have}\:{found}\:\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Commented by Olaf last updated on 25/Dec/20
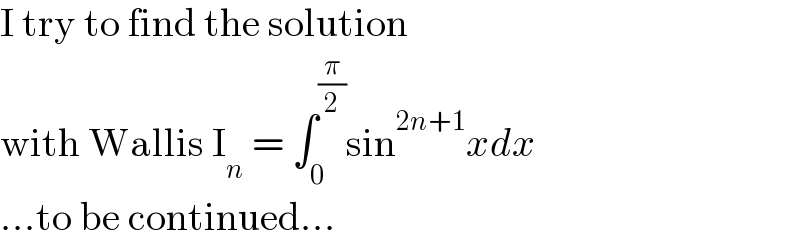
$$\mathrm{I}\:\mathrm{try}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{solution} \\ $$$$\mathrm{with}\:\mathrm{Wallis}\:\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}{n}+\mathrm{1}} {xdx} \\ $$$$…\mathrm{to}\:\mathrm{be}\:\mathrm{continued}… \\ $$
Commented by Dwaipayan Shikari last updated on 25/Dec/20
![I have tried Σ_(n=0) ^∞ ((n!^2 )/((2n+1)!))=Σ_(n=0) ^∞ ((Γ^2 (n+1))/(Γ(2n+2)))=Σ_(n=0) ^∞ B(n+1,n+1) =Σ_(n=0) ^∞ ∫_0 ^1 x^n (1−x)^n =∫_0 ^1 Σ_(n=0) ^∞ x^n (1−x)^n =∫_0 ^1 (1/(1−x(1−x)))dx =∫_0 ^1 (1/(x^2 −x+1))dx=[(2/( (√3)))tan^(−1) ((2x−1)/( (√3)))]_0 ^1 =((2π)/( 3(√3)))](https://www.tinkutara.com/question/Q126942.png)
$${I}\:{have}\:{tried} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}!^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\Gamma^{\mathrm{2}} \left({n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{2}{n}+\mathrm{2}\right)}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{B}\left({n}+\mathrm{1},{n}+\mathrm{1}\right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left(\mathrm{1}−{x}\right)^{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \left(\mathrm{1}−{x}\right)^{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{x}\left(\mathrm{1}−{x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}=\left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}\pi}{\:\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Answered by mindispower last updated on 25/Dec/20
![=Σ_(n≥0) ((n!.n!)/((2n+1)!))=Σ_(n≥0) ((Γ(n+1)Γ(n+1))/(Γ(2n+2)_ )) =Σ_(n≥0) β(n+1,n+1)=Σ_(n≥0) ∫_0 ^1 t^(n−1) (1−t)^(n−1) dt =∫_0 ^1 Σ_(n≥0) (t(1−t))^(n−1) dt =∫_0 ^1 (1/(1−t+t^2 ))dt =∫_0 ^1 (1/((t−(1/2))^2 +(3/4)))dt =∫_0 ^1 (dt/((3/4)((((2t−1)/( (√3))))^2 +1)))=[_0 ^1 (2/( (√3)))tan^− (((2t−1)/( (√3))))] =(4/( (√3)))tan^− ((1/( (√3))))=4(π/(6(√3)))=((2π)/(3(√3)))](https://www.tinkutara.com/question/Q126943.png)
$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{n}!.{n}!}{\left(\mathrm{2}{n}+\mathrm{1}\right)!}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\Gamma\left({n}+\mathrm{1}\right)\Gamma\left({n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{2}{n}+\mathrm{2}\right)_{} } \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\beta\left({n}+\mathrm{1},{n}+\mathrm{1}\right)=\underset{{n}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{n}−\mathrm{1}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{0}} {\sum}\left({t}\left(\mathrm{1}−{t}\right)\right)^{{n}−\mathrm{1}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{t}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\frac{\mathrm{3}}{\mathrm{4}}\left(\left(\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}\right)}=\left[_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−} \left(\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right] \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}{tan}^{−} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)=\mathrm{4}\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Dec/20

$${Thanking}\:{you} \\ $$
