Question Number 128566 by Dwaipayan Shikari last updated on 08/Jan/21
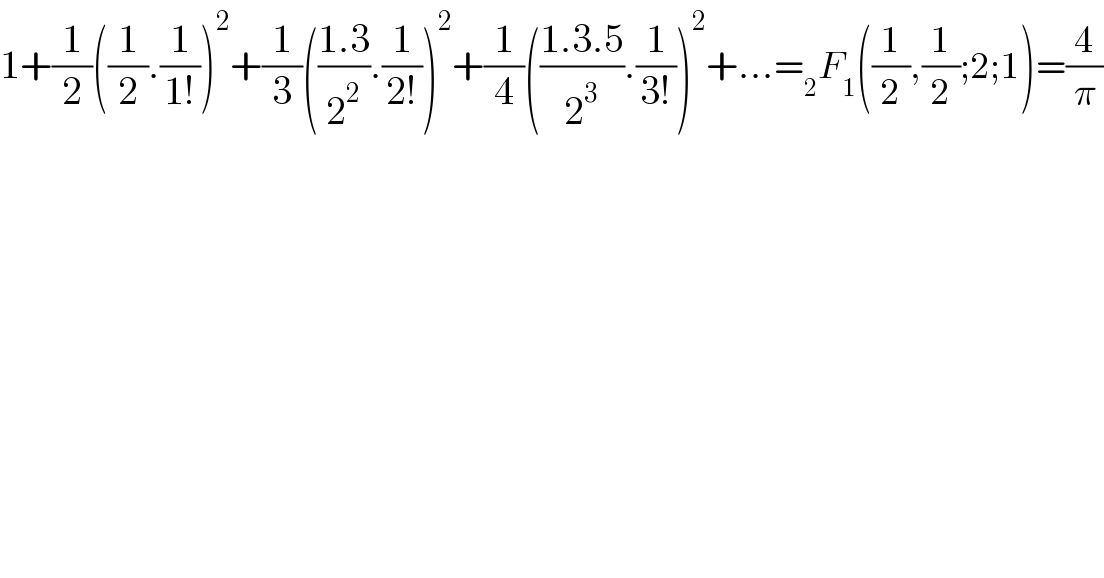
$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{1}!}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}.\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }.\frac{\mathrm{1}}{\mathrm{2}!}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}}{\mathrm{2}^{\mathrm{3}} }.\frac{\mathrm{1}}{\mathrm{3}!}\right)^{\mathrm{2}} +…=_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\mathrm{2};\mathrm{1}\right)=\frac{\mathrm{4}}{\pi} \\ $$
Commented by Dwaipayan Shikari last updated on 08/Jan/21
I've posted this question on brilliant
https://brilliant.org/problems/in-search-of
