Menu Close

1-1-2-1-2-3-1-3-5-1-4-7-1-5-11-1-6-13-

Tinku Tara 0 Comments
Pin




Question Number 126200 by Dwaipayan Shikari last updated on 18/Dec/20
(1/1^2 )−(1/2^3 )+(1/3^5 )−(1/4^7 )+(1/5^(11) )−(1/6^(13) )+....
$$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{5}} }−\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{11}} }−\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{13}} }+…. \\ $$
Commented by Olaf last updated on 18/Dec/20
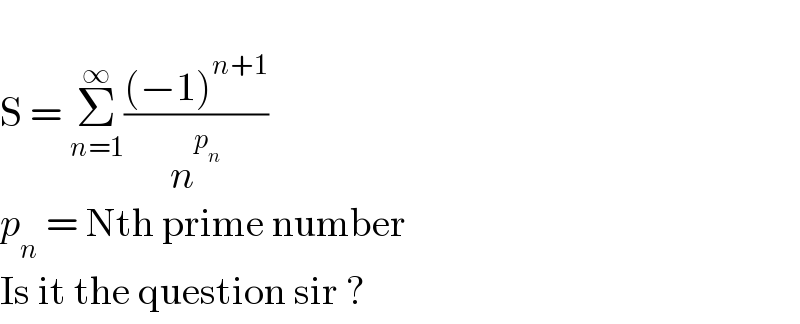
S = Σ_(n=1) ^∞ (((−1)^(n+1) )/n^p_n ) p_n = Nth prime number Is it the question sir ?
$$ \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}^{{p}_{{n}} } } \\ $$$${p}_{{n}} \:=\:\mathrm{Nth}\:\mathrm{prime}\:\mathrm{number} \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{the}\:\mathrm{question}\:\mathrm{sir}\:? \\ $$
Commented by Dwaipayan Shikari last updated on 18/Dec/20
yes sir!
$${yes}\:{sir}! \\ $$
Commented by Olaf last updated on 18/Dec/20
I have no idea how to calculate this but maybe we can find lower and upper bounds : p_n Nth prime number 1, 2, 3, 5, 7, 11, 13... Felgner result in 1990 : 0,91nlnn < p_n <1,7nlnn S = Σ_(n=2) ^∞ (((−1)^n )/((n−1)^p_n )) Σ_(n=2) ^∞ (((−1)^n )/((n−1)^(1,7nlnn) )) < S < Σ_(n=2) ^∞ (((−1)^n )/((n−1)^(0,91nlnn) )) ... I don′t know if it is a good way.
$$ \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{idea}\:\mathrm{how}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{this}\:\mathrm{but} \\ $$$$\mathrm{maybe}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{lower}\:\mathrm{and}\:\mathrm{upper} \\ $$$$\mathrm{bounds}\:: \\ $$$${p}_{{n}} \:\mathrm{Nth}\:\mathrm{prime}\:\mathrm{number} \\ $$$$\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{5},\:\mathrm{7},\:\mathrm{11},\:\mathrm{13}… \\ $$$$ \\ $$$$\mathrm{Felgner}\:\mathrm{result}\:\mathrm{in}\:\mathrm{1990}\:: \\ $$$$\mathrm{0},\mathrm{91}{n}\mathrm{ln}{n}\:<\:{p}_{{n}} \:<\mathrm{1},\mathrm{7}{n}\mathrm{ln}{n} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}−\mathrm{1}\right)^{{p}_{{n}} } } \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}−\mathrm{1}\right)^{\mathrm{1},\mathrm{7}{n}\mathrm{ln}{n}} }\:<\:\mathrm{S}\:<\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}−\mathrm{1}\right)^{\mathrm{0},\mathrm{91}{n}\mathrm{ln}{n}} } \\ $$$$… \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{if}\:\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{good}\:\mathrm{way}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *