Question Number 99889 by Dwaipayan Shikari last updated on 23/Jun/20

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{7}}+…….\infty\left\{\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\right\} \\ $$
Answered by smridha last updated on 23/Jun/20

$$\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{called}}\:\boldsymbol{{H}}{a}\boldsymbol{{rmonic}}\:\boldsymbol{{series}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{H}}{a}\boldsymbol{{rmonic}}\:\boldsymbol{{series}}\:\boldsymbol{{always}} \\ $$$$\boldsymbol{{diverge}}\:\boldsymbol{{so}}\:\boldsymbol{{it}}\:\boldsymbol{{has}}\:\boldsymbol{{no}}\:\boldsymbol{{finite}}\:\boldsymbol{{value}} \\ $$$$\boldsymbol{{H}}_{\boldsymbol{{n}}} =\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{{n}}}=\infty \\ $$$$\boldsymbol{{if}}\:\boldsymbol{{the}}\:\boldsymbol{{series}}\:\boldsymbol{{is}}\:\boldsymbol{{like}}\:\boldsymbol{{that}}: \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+…\infty=\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\left(\mathrm{1}\right)^{\boldsymbol{{n}}} \\ $$$$=\boldsymbol{{ln}}\left(\mathrm{2}\right)\approx\mathrm{0}.\mathrm{693} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jun/20
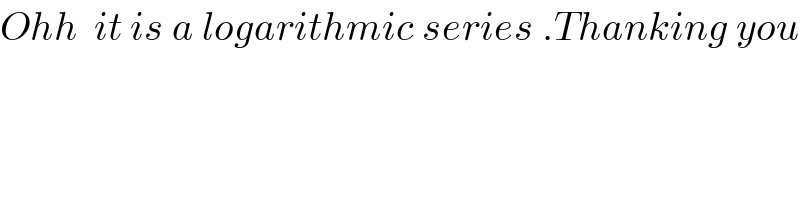
$${Ohh}\:\:{it}\:{is}\:{a}\:{logarithmic}\:{series}\:.{Thanking}\:{you} \\ $$
