Question Number 161907 by bobhans last updated on 24/Dec/21
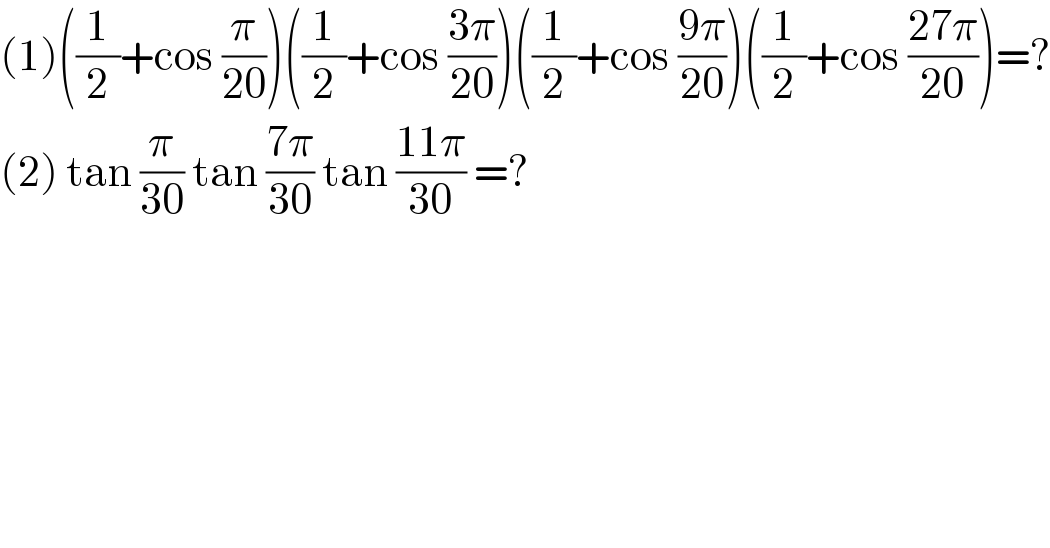
$$\left(\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\pi}{\mathrm{20}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{20}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{9}\pi}{\mathrm{20}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{27}\pi}{\mathrm{20}}\right)=? \\ $$$$\left(\mathrm{2}\right)\:\mathrm{tan}\:\frac{\pi}{\mathrm{30}}\:\mathrm{tan}\:\frac{\mathrm{7}\pi}{\mathrm{30}}\:\mathrm{tan}\:\frac{\mathrm{11}\pi}{\mathrm{30}}\:=? \\ $$
Commented by blackmamba last updated on 24/Dec/21
![(π/(20)) = 9° ; G=((1/2)+cos 9°)((1/2)+cos 27°)((1/2)+cos 81°)((1/2)+cos 243°) [ { ((cos 81°=sin 9°)),((cos 243°=−sin 27° )) :}] G=((1/2)+cos 9°)((1/2)+cos 27°)((1/2)+sin 9°)((1/2)−sin 27°) 16G= (1+2cos 9°)(1+2cos 27°)(1+2sin 9°)(1−2sin 27°) 16G=(1+2cos 9°+2sin 9°+2sin 18°)(1−2sin 27°+2cos 27°−2sin 54°)](https://www.tinkutara.com/question/Q161909.png)
$$\:\frac{\pi}{\mathrm{20}}\:=\:\mathrm{9}°\:;\:{G}=\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\mathrm{9}°\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\mathrm{27}°\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\mathrm{81}°\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\mathrm{243}°\right) \\ $$$$\:\left[\:\begin{cases}{\mathrm{cos}\:\mathrm{81}°=\mathrm{sin}\:\mathrm{9}°}\\{\mathrm{cos}\:\mathrm{243}°=−\mathrm{sin}\:\mathrm{27}°\:}\end{cases}\right] \\ $$$$\:{G}=\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\mathrm{9}°\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\mathrm{27}°\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{sin}\:\mathrm{9}°\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\mathrm{27}°\right) \\ $$$$\:\mathrm{16}{G}=\:\left(\mathrm{1}+\mathrm{2cos}\:\mathrm{9}°\right)\left(\mathrm{1}+\mathrm{2cos}\:\mathrm{27}°\right)\left(\mathrm{1}+\mathrm{2sin}\:\mathrm{9}°\right)\left(\mathrm{1}−\mathrm{2sin}\:\mathrm{27}°\right) \\ $$$$\:\mathrm{16}{G}=\left(\mathrm{1}+\mathrm{2cos}\:\mathrm{9}°+\mathrm{2sin}\:\mathrm{9}°+\mathrm{2sin}\:\mathrm{18}°\right)\left(\mathrm{1}−\mathrm{2sin}\:\mathrm{27}°+\mathrm{2cos}\:\mathrm{27}°−\mathrm{2sin}\:\mathrm{54}°\right) \\ $$$$ \\ $$
