Question Number 127908 by bramlexs22 last updated on 03/Jan/21
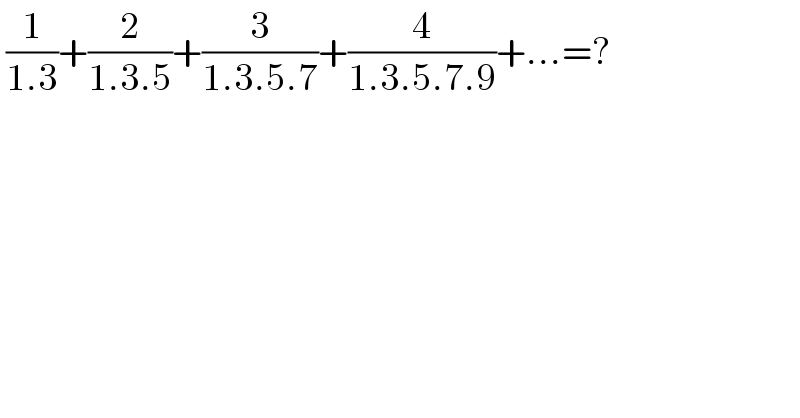
$$\:\frac{\mathrm{1}}{\mathrm{1}.\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{1}.\mathrm{3}.\mathrm{5}}+\frac{\mathrm{3}}{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}}+\frac{\mathrm{4}}{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}.\mathrm{9}}+…=? \\ $$
Answered by liberty last updated on 03/Jan/21

$$\:\mathrm{Let}\:\lambda\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{n}}{\mathrm{1}.\mathrm{3}.\mathrm{5}…\left(\mathrm{2n}+\mathrm{1}\right)}\: \\ $$$$\mathrm{consider}\:\frac{\mathrm{n}}{\mathrm{1}.\mathrm{3}.\mathrm{5}….\left(\mathrm{2n}+\mathrm{1}\right)}\:=\:\frac{\mathrm{n}}{\mathrm{1}.\left(\mathrm{3}.\mathrm{5}…\left(\mathrm{2n}−\mathrm{1}\right)\right).\left(\mathrm{2n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\:\frac{\left(\mathrm{2n}+\mathrm{1}\right)−\mathrm{1}}{\mathrm{1}.\left(\mathrm{3}.\mathrm{5}…\left(\mathrm{2n}−\mathrm{1}\right)\right).\left(\mathrm{2n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}.\mathrm{3}.\mathrm{5}…\left(\mathrm{2n}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{5}….\left(\mathrm{2n}+\mathrm{1}\right)}\right) \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{get}\:\lambda\:=\:\underset{\mathrm{k}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{1}.\mathrm{3}.\mathrm{5}….\left(\mathrm{2n}−\mathrm{1}\right)}−\:\frac{\mathrm{1}}{\mathrm{3}.\mathrm{5}….\left(\mathrm{2n}+\mathrm{1}\right)}\right) \\ $$$$\mathrm{telescoping}\:\mathrm{series} \\ $$$$\lambda\:=\:\underset{\mathrm{k}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\mathrm{1}}\:−\:\frac{\mathrm{1}}{\mathrm{3}.\mathrm{5}….\left(\mathrm{2k}+\mathrm{1}\right)}\:\right) \\ $$$$\lambda\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{0}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
