Question Number 124892 by Dwaipayan Shikari last updated on 06/Dec/20
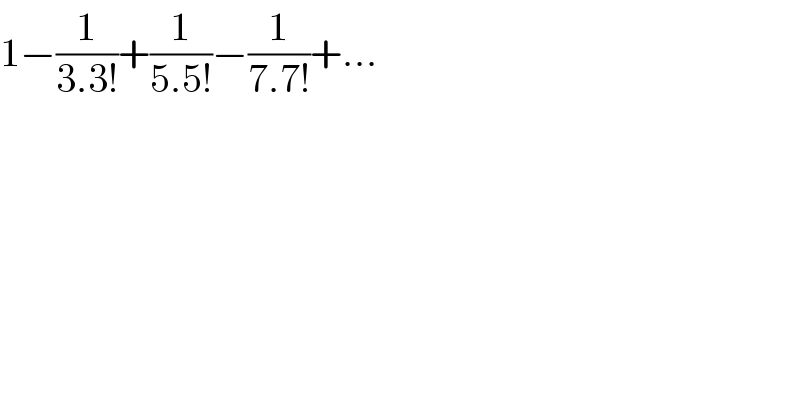
$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{5}.\mathrm{5}!}−\frac{\mathrm{1}}{\mathrm{7}.\mathrm{7}!}+… \\ $$
Commented by Dwaipayan Shikari last updated on 06/Dec/20
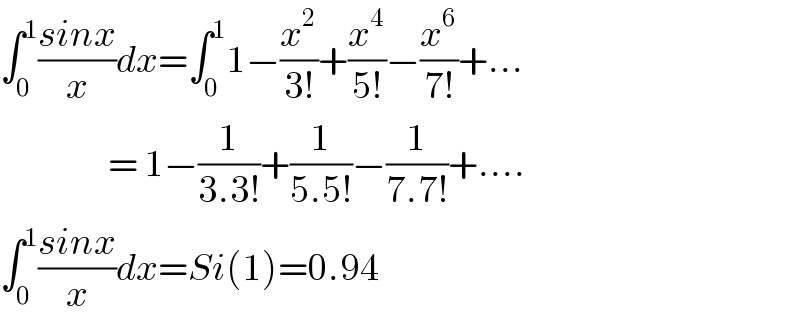
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sinx}}{{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{5}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{7}!}+… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{5}.\mathrm{5}!}−\frac{\mathrm{1}}{\mathrm{7}.\mathrm{7}!}+…. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sinx}}{{x}}{dx}={Si}\left(\mathrm{1}\right)=\mathrm{0}.\mathrm{94} \\ $$
Commented by mnjuly1970 last updated on 06/Dec/20
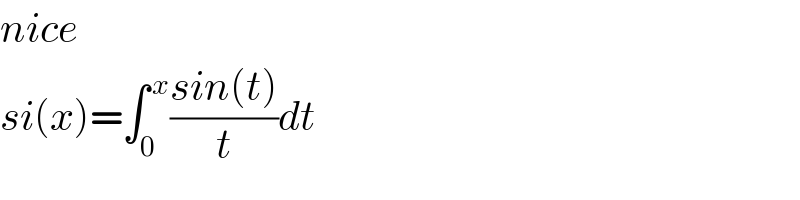
$${nice} \\ $$$${si}\left({x}\right)=\int_{\mathrm{0}} ^{\:{x}} \frac{{sin}\left({t}\right)}{{t}}{dt} \\ $$
