Question Number 52619 by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19
![1)∫_1 ^3 (dx/(x^2 +[x]^2 +1−2x[x])) 2)∫_(−1) ^1 [x[1+sinπx]+1]dx 3)∫_0 ^2 x^([x^2 +1]) dx 4)∫_0 ^1 e^(2x−[2x]) d(x−[x]) 5)∫_(−2) ^3 ∣x^2 −5x−6∣dx from question 1 to 4 [.]←greatest integer fuction ∣.∣←mod questions taken from B.Stat entrance exam...](https://www.tinkutara.com/question/Q52619.png)
$$\left.\mathrm{1}\right)\int_{\mathrm{1}} ^{\mathrm{3}} \frac{{dx}}{{x}^{\mathrm{2}} +\left[{x}\right]^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}\left[{x}\right]} \\ $$$$\left.\mathrm{2}\right)\int_{−\mathrm{1}} ^{\mathrm{1}} \left[{x}\left[\mathrm{1}+{sin}\pi{x}\right]+\mathrm{1}\right]{dx} \\ $$$$\left.\mathrm{3}\right)\int_{\mathrm{0}} ^{\mathrm{2}} {x}^{\left[{x}^{\mathrm{2}} +\mathrm{1}\right]} {dx} \\ $$$$\left.\mathrm{4}\right)\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\mathrm{2}{x}−\left[\mathrm{2}{x}\right]} {d}\left({x}−\left[{x}\right]\right)\: \\ $$$$\left.\mathrm{5}\right)\int_{−\mathrm{2}} ^{\mathrm{3}} \mid{x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{6}\mid{dx} \\ $$$${from}\:{question}\:\mathrm{1}\:{to}\:\mathrm{4}\:\left[.\right]\leftarrow{greatest}\:{integer}\:{fuction} \\ $$$$\mid.\mid\leftarrow{mod} \\ $$$${questions}\:{taken}\:{from}\:{B}.{Stat}\:{entrance}\:{exam}… \\ $$
Commented by maxmathsup by imad last updated on 10/Jan/19
![1) let I =∫_1 ^3 (dx/(x^2 +[x]^2 +1−2x[x])) ⇒ I =∫_1 ^3 (dx/((x−[x])^2 +1)) =∫_1 ^2 (dx/((x−1)^2 +1))+ ∫_2 ^3 (dx/((x−2)^2 +1)) but ∫_1 ^2 (dx/((x−1)^2 +1)) =_(x−1=t ) ∫_0 ^1 (dt/(t^2 +1)) =[arctan(t)]_0 ^1 =(π/4) ∫_2 ^3 (dx/((x−2)^2 +1)) =_(x−2=t) ∫_0 ^1 (dt/(t^2 +1)) =(π/4) ⇒ I =(π/2) .](https://www.tinkutara.com/question/Q52624.png)
$$\left.\mathrm{1}\right)\:{let}\:{I}\:=\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\frac{{dx}}{{x}^{\mathrm{2}} +\left[{x}\right]^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}\left[{x}\right]}\:\Rightarrow\:{I}\:=\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\:\frac{{dx}}{\left({x}−\left[{x}\right]\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}+\:\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\:\frac{{dx}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}}\:{but} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:=_{{x}−\mathrm{1}={t}\:} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\left[{arctan}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\:\frac{{dx}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}}\:=_{{x}−\mathrm{2}={t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\pi}{\mathrm{4}}\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{2}}\:. \\ $$
Commented by maxmathsup by imad last updated on 10/Jan/19
![2) let A=∫_(−1) ^1 [x[1+sin(πx)]+1]dx ⇒ A =∫_(−1) ^1 [x +x[sin(πx)]+1]dx=∫_(−1) ^1 [x+1 +x[sin(πx)]]dx =_(x+1 =t) ∫_0 ^2 [t +(t−1)[−sin(πt)] dt =∫_0 ^1 [t+(t−1)[−sin(πt)]]dt +∫_1 ^2 [t+(t−1)[−sin(πt)]dt but ∫_0 ^1 [t+(t−1)[−sin(πt)]]dt=∫_0 ^(1/2) [t+(t−1)(0)]dt+∫_(1/2) ^1 [t+(t−1)(0)]dt =∫_0 ^(1/2) [t]dt +∫_(1/2) ^1 [t]dt =0 +0 =0 ∫_1 ^2 [t+(t−1)[−sin(πt)]]dt = ∫_1 ^(3/2) [t +(t−1)(−1)]dt +∫_(3/2) ^2 [t +(t−1)(−1)]dt =∫_1 ^(3/2) [1]dt +∫_(3/2) ^2 [1] dt =(3/2) −1 +2−(3/2) =1 ⇒ A =1 +(perhaps)^2 ....](https://www.tinkutara.com/question/Q52625.png)
$$\left.\mathrm{2}\right)\:\:{let}\:{A}=\int_{−\mathrm{1}} ^{\mathrm{1}} \left[{x}\left[\mathrm{1}+{sin}\left(\pi{x}\right)\right]+\mathrm{1}\right]{dx}\:\Rightarrow \\ $$$${A}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\left[{x}\:+{x}\left[{sin}\left(\pi{x}\right)\right]+\mathrm{1}\right]{dx}=\int_{−\mathrm{1}} ^{\mathrm{1}} \left[{x}+\mathrm{1}\:+{x}\left[{sin}\left(\pi{x}\right)\right]\right]{dx} \\ $$$$=_{{x}+\mathrm{1}\:={t}} \:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\left[{t}\:+\left({t}−\mathrm{1}\right)\left[−{sin}\left(\pi{t}\right)\right]\:{dt}\right. \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left[{t}+\left({t}−\mathrm{1}\right)\left[−{sin}\left(\pi{t}\right)\right]\right]{dt}\:+\int_{\mathrm{1}} ^{\mathrm{2}} \left[{t}+\left({t}−\mathrm{1}\right)\left[−{sin}\left(\pi{t}\right)\right]{dt}\:{but}\right. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left[{t}+\left({t}−\mathrm{1}\right)\left[−{sin}\left(\pi{t}\right)\right]\right]{dt}=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\left[{t}+\left({t}−\mathrm{1}\right)\left(\mathrm{0}\right)\right]{dt}+\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \left[{t}+\left({t}−\mathrm{1}\right)\left(\mathrm{0}\right)\right]\boldsymbol{{dt}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left[{t}\right]{dt}\:\:+\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \left[{t}\right]{dt}\:=\mathrm{0}\:+\mathrm{0}\:=\mathrm{0} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \left[{t}+\left({t}−\mathrm{1}\right)\left[−{sin}\left(\pi{t}\right)\right]\right]{dt}\:=\:\int_{\mathrm{1}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \left[{t}\:+\left({t}−\mathrm{1}\right)\left(−\mathrm{1}\right)\right]\boldsymbol{{dt}}\:+\int_{\frac{\mathrm{3}}{\mathrm{2}}} ^{\mathrm{2}} \left[{t}\:+\left({t}−\mathrm{1}\right)\left(−\mathrm{1}\right)\right]{dt} \\ $$$$=\int_{\mathrm{1}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \left[\mathrm{1}\right]{dt}\:+\int_{\frac{\mathrm{3}}{\mathrm{2}}} ^{\mathrm{2}} \left[\mathrm{1}\right]\:{dt}\:=\frac{\mathrm{3}}{\mathrm{2}}\:−\mathrm{1}\:+\mathrm{2}−\frac{\mathrm{3}}{\mathrm{2}}\:=\mathrm{1}\:\:\Rightarrow\:{A}\:=\mathrm{1}\:+\left({perhaps}\right)^{\mathrm{2}} …. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19

$${thankyou}\:{sir}.. \\ $$
Commented by Abdo msup. last updated on 10/Jan/19
![4) changement 2x=t give ∫_0 ^1 e^(2x−[2x]) d(x−[x])=∫_0 ^2 e^(t−[t]) d((t/2) −[(t/2)]) =∫_0 ^1 e^(t−[t]) d((t/2) −[(t/2)])+∫_1 ^2 e^(t−[t]) d((t/2)−[(t/2)]) =∫_0 ^1 e^t (dt/2) +∫_1 ^2 e^(t−1) (dt/2) =(1/2)[e^t ]_0 ^1 +(1/(2e))[e^t ]_1 ^2 =(1/2)(e−1) +(1/(2e))(e^2 −1) .](https://www.tinkutara.com/question/Q52647.png)
$$\left.\mathrm{4}\right)\:{changement}\:\mathrm{2}{x}={t}\:{give}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{\mathrm{2}{x}−\left[\mathrm{2}{x}\right]} {d}\left({x}−\left[{x}\right]\right)=\int_{\mathrm{0}} ^{\mathrm{2}} \:\:{e}^{{t}−\left[{t}\right]} {d}\left(\frac{{t}}{\mathrm{2}}\:−\left[\frac{{t}}{\mathrm{2}}\right]\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{{t}−\left[{t}\right]} {d}\left(\frac{{t}}{\mathrm{2}}\:−\left[\frac{{t}}{\mathrm{2}}\right]\right)+\int_{\mathrm{1}} ^{\mathrm{2}} \:{e}^{{t}−\left[{t}\right]} {d}\left(\frac{{t}}{\mathrm{2}}−\left[\frac{{t}}{\mathrm{2}}\right]\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{t}} \frac{{dt}}{\mathrm{2}}\:+\int_{\mathrm{1}} ^{\mathrm{2}} \:{e}^{{t}−\mathrm{1}} \frac{{dt}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{e}^{{t}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2}{e}}\left[{e}^{{t}} \right]_{\mathrm{1}} ^{\mathrm{2}} \:=\frac{\mathrm{1}}{\mathrm{2}}\left({e}−\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}{e}}\left({e}^{\mathrm{2}} −\mathrm{1}\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19
![3)∫_0 ^2 x^([x^2 +1]) dx ∫_0 ^1 xdx+∫_1 ^(√2) x^2 dx+∫_(√2) ^(√3) x^3 dx+∫_(√3) ^2 x^4 dx now it can be solved...attaching graph for clarity..](https://www.tinkutara.com/question/Q52633.png)
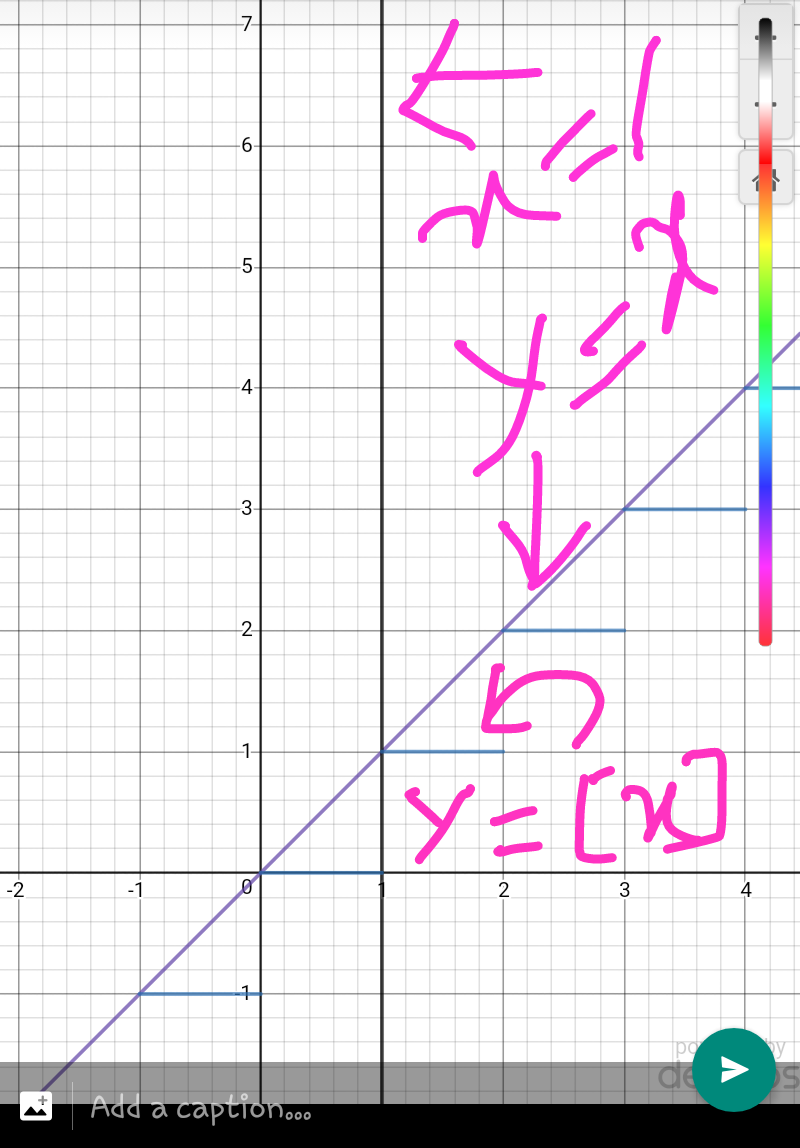
$$\left.\mathrm{3}\right)\int_{\mathrm{0}} ^{\mathrm{2}} {x}^{\left[{x}^{\mathrm{2}} +\mathrm{1}\right]} {dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {xdx}+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} {x}^{\mathrm{2}} {dx}+\int_{\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{3}}} {x}^{\mathrm{3}} {dx}+\int_{\sqrt{\mathrm{3}}} ^{\mathrm{2}} {x}^{\mathrm{4}} {dx} \\ $$$${now}\:{it}\:{can}\:{be}\:{solved}…{attaching}\:{graph}\:{for}\:{clarity}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19
![for 1>x≥0 [x^2 +1]=1 (√2) >x≥1 [x^2 +1]=2 (√3) >x≥(√2) [x^2 +1]=3 2>x≥(√3) [x^2 +1]=4](https://www.tinkutara.com/question/Q52637.png)
$$\:{for}\:\mathrm{1}>{x}\geqslant\mathrm{0}\:\:\left[{x}^{\mathrm{2}} +\mathrm{1}\right]=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{2}}\:>{x}\geqslant\mathrm{1}\:\:\left[{x}^{\mathrm{2}} +\mathrm{1}\right]=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{3}}\:>{x}\geqslant\sqrt{\mathrm{2}}\:\:\left[{x}^{\mathrm{2}} +\mathrm{1}\right]=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}>{x}\geqslant\sqrt{\mathrm{3}}\:\:\:\:\:\left[{x}^{\mathrm{2}} +\mathrm{1}\right]=\mathrm{4} \\ $$
Answered by ajfour last updated on 10/Jan/19
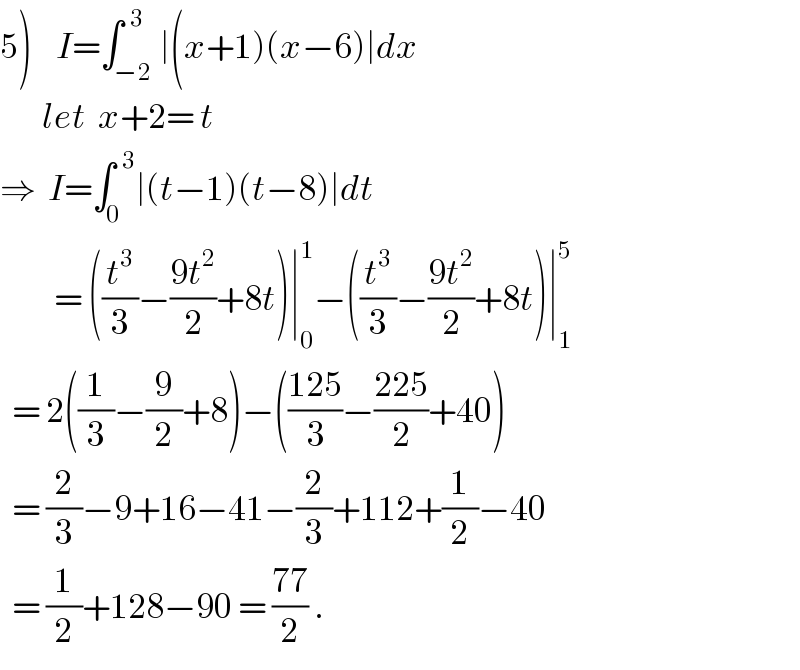
$$\left.\mathrm{5}\right)\:\:\:\:{I}=\int_{−\mathrm{2}} ^{\:\:\mathrm{3}} \mid\left({x}+\mathrm{1}\right)\left({x}−\mathrm{6}\right)\mid{dx} \\ $$$$\:\:\:\:\:\:\:{let}\:\:{x}+\mathrm{2}=\:{t} \\ $$$$\Rightarrow\:\:{I}=\int_{\mathrm{0}} ^{\:\:\mathrm{3}} \mid\left({t}−\mathrm{1}\right)\left({t}−\mathrm{8}\right)\mid{dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\left(\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{9}{t}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{8}{t}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} −\left(\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{9}{t}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{8}{t}\right)\mid_{\mathrm{1}} ^{\mathrm{5}} \\ $$$$\:\:=\:\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{9}}{\mathrm{2}}+\mathrm{8}\right)−\left(\frac{\mathrm{125}}{\mathrm{3}}−\frac{\mathrm{225}}{\mathrm{2}}+\mathrm{40}\right) \\ $$$$\:\:=\:\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{9}+\mathrm{16}−\mathrm{41}−\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{112}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{40} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{128}−\mathrm{90}\:=\:\frac{\mathrm{77}}{\mathrm{2}}\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19

$${thank}\:{you}\:{sir}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19
![4)∫_0 ^1 e^(2x−[2x]) d(x−[x]) [2x]=0 (1/2)>x≥0 [x]=0 (1/2)>x≥0 [2x]= 1 1>x≥(1/2) [x]=0 ∫_0 ^(1/2) e^(2x−0) d(x−0)+∫_(1/2) ^1 e^(2x−1) d(x−0) =∫_0 ^(1/2) e^(2x) dx+∫_(1/2) ^1 e^(2x−1) dx now can be solved...](https://www.tinkutara.com/question/Q52638.png)
$$\left.\mathrm{4}\right)\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\mathrm{2}{x}−\left[\mathrm{2}{x}\right]} {d}\left({x}−\left[{x}\right]\right) \\ $$$$\left[\mathrm{2}{x}\right]=\mathrm{0}\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}>{x}\geqslant\mathrm{0}\:\: \\ $$$$\left[{x}\right]=\mathrm{0}\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}>{x}\geqslant\mathrm{0} \\ $$$$\left[\mathrm{2}{x}\right]=\:\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{1}>{x}\geqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left[{x}\right]=\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {e}^{\mathrm{2}{x}−\mathrm{0}} {d}\left({x}−\mathrm{0}\right)+\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:{e}^{\mathrm{2}{x}−\mathrm{1}} {d}\left({x}−\mathrm{0}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {e}^{\mathrm{2}{x}} {dx}+\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} {e}^{\mathrm{2}{x}−\mathrm{1}} {dx} \\ $$$${now}\:{can}\:{be}\:{solved}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19