Question Number 100000 by Dwaipayan Shikari last updated on 24/Jun/20

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{32}}+\frac{\mathrm{1}}{\mathrm{243}}+\frac{\mathrm{1}}{\mathrm{1024}}+…\infty \\ $$
Commented by ajfour last updated on 27/Jun/20
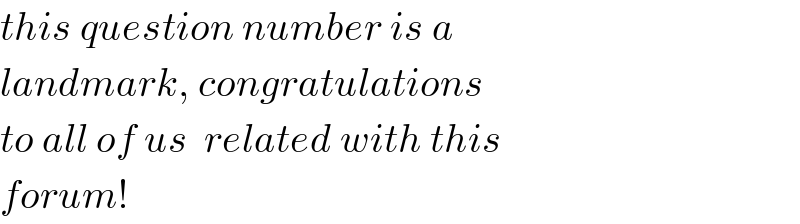
$${this}\:{question}\:{number}\:{is}\:{a}\: \\ $$$${landmark},\:{congratulations} \\ $$$${to}\:{all}\:{of}\:{us}\:\:{related}\:{with}\:{this}\: \\ $$$${forum}! \\ $$
Answered by maths mind last updated on 24/Jun/20

$$=\underset{{n}\in\mathbb{N}^{\ast} } {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{5}} }=\zeta\left(\mathrm{5}\right) \\ $$
Answered by smridha last updated on 24/Jun/20

$$\boldsymbol{\zeta}\left(\mathrm{5}\right)\approx\mathrm{1}.\mathrm{03692}……. \\ $$
Commented by Rio Michael last updated on 24/Jun/20
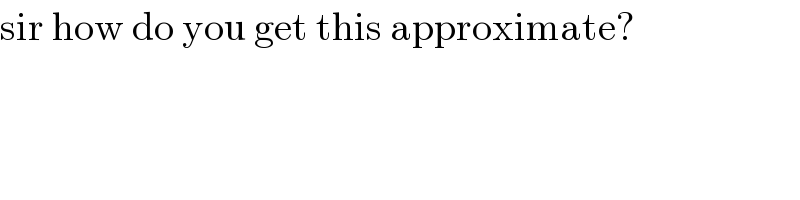
$$\mathrm{sir}\:\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{get}\:\mathrm{this}\:\mathrm{approximate}? \\ $$
Commented by smridha last updated on 24/Jun/20

$$\boldsymbol{{i}}\:\boldsymbol{{just}}\:\boldsymbol{{put}}\:\boldsymbol{{it}}\:\boldsymbol{{from}}\:\boldsymbol{{table}}… \\ $$$$\boldsymbol{{I}}\:\:\boldsymbol{{know}}\:\boldsymbol{{all}}\:\boldsymbol{{the}}\:\boldsymbol{{calculations}}\:\boldsymbol{{but}} \\ $$$$\boldsymbol{{it}}'{s}\:\boldsymbol{{too}}\:\boldsymbol{{lengthy}}…\boldsymbol{{mostly}}\:\boldsymbol{{for}}\: \\ $$$$\boldsymbol{\zeta}\left(\mathrm{2}\boldsymbol{{n}}+\mathrm{1}\right)\:\boldsymbol{{where}}\:\boldsymbol{{n}}=\mathrm{1},\mathrm{2},\mathrm{3}…… \\ $$
Commented by Rio Michael last updated on 24/Jun/20
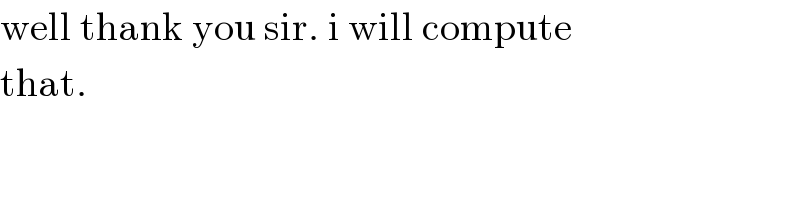
$$\mathrm{well}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{compute} \\ $$$$\mathrm{that}. \\ $$
