Question Number 152588 by rexford last updated on 30/Aug/21
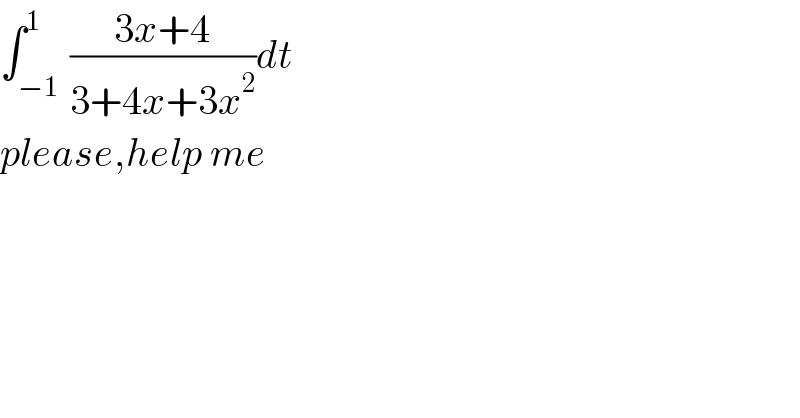
$$\int_{−\mathrm{1}\:} ^{\mathrm{1}} \frac{\mathrm{3}{x}+\mathrm{4}}{\mathrm{3}+\mathrm{4}{x}+\mathrm{3}{x}^{\mathrm{2}} }{dt} \\ $$$${please},{help}\:{me} \\ $$
Answered by qaz last updated on 30/Aug/21
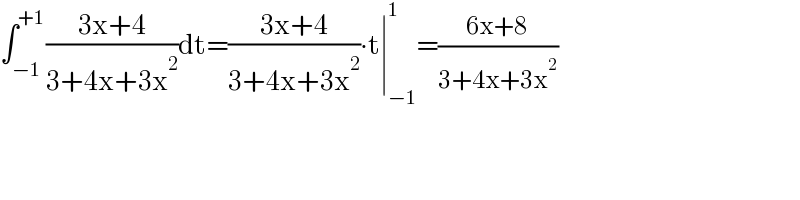
$$\int_{−\mathrm{1}} ^{+\mathrm{1}} \frac{\mathrm{3x}+\mathrm{4}}{\mathrm{3}+\mathrm{4x}+\mathrm{3x}^{\mathrm{2}} }\mathrm{dt}=\frac{\mathrm{3x}+\mathrm{4}}{\mathrm{3}+\mathrm{4x}+\mathrm{3x}^{\mathrm{2}} }\centerdot\mathrm{t}\mid_{−\mathrm{1}} ^{\mathrm{1}} =\frac{\mathrm{6x}+\mathrm{8}}{\mathrm{3}+\mathrm{4x}+\mathrm{3x}^{\mathrm{2}} } \\ $$
Answered by puissant last updated on 30/Aug/21
![=(1/2)∫_(−1) ^1 ((6x+4+4)/(3x^2 +4x+3))dx = (1/2)∫_(−1) ^1 ((6x+4)/(3x^2 +4x+3))dx+(2/3)∫_(−1) ^(+1) (1/(x^2 +(4/3)x+1))dx =(1/2)[ln∣3x^2 +4x+3∣]_(−1) ^1 +(2/3)Q =(1/2)ln5+(2/3)Q Q=∫_(−1) ^1 (1/(x^2 +(4/3)x+1))dx = ∫_(−1) ^1 (1/((x+(2/3))^2 −(4/9)+(9/9)))dx =∫_(−1) ^1 (1/((x+(2/3))^2 +(5/9)))dx =(9/5)∫_(−1) ^1 (1/([((3/( (√5)))(x+(2/3)))^2 +1]))dx u=(3/( (√5)))(x+(2/3)) → dx=((√5)/3)du ⇒ Q=(9/5)×((√5)/3)∫_(−1) ^1 (1/(u^2 +1))du =(3/( (√5)))[arctan(u)]_(−1) ^1 = (3/( (√5)))×(π/2). ∴∵ I=(1/2)ln5+(3/( (√5)))×(2/3)×(π/2) = (1/2)ln5+(π/( (√5)))..](https://www.tinkutara.com/question/Q152589.png)
$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{6}{x}+\mathrm{4}+\mathrm{4}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}}{dx}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{6}{x}+\mathrm{4}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}}{dx}+\frac{\mathrm{2}}{\mathrm{3}}\int_{−\mathrm{1}} ^{+\mathrm{1}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{3}}{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}\mid\right]_{−\mathrm{1}} ^{\mathrm{1}} +\frac{\mathrm{2}}{\mathrm{3}}{Q} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{5}+\frac{\mathrm{2}}{\mathrm{3}}{Q} \\ $$$${Q}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{3}}{x}+\mathrm{1}}{dx}\:=\:\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({x}+\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{9}}+\frac{\mathrm{9}}{\mathrm{9}}}{dx} \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({x}+\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{9}}}{dx}\:=\frac{\mathrm{9}}{\mathrm{5}}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left[\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\left({x}+\frac{\mathrm{2}}{\mathrm{3}}\right)\right)^{\mathrm{2}} +\mathrm{1}\right]}{dx} \\ $$$${u}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\left({x}+\frac{\mathrm{2}}{\mathrm{3}}\right)\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}{du} \\ $$$$\Rightarrow\:{Q}=\frac{\mathrm{9}}{\mathrm{5}}×\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}{du} \\ $$$$=\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\left[{arctan}\left({u}\right)\right]_{−\mathrm{1}} ^{\mathrm{1}} =\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}×\frac{\pi}{\mathrm{2}}. \\ $$$$\therefore\because\:\:{I}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{5}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}×\frac{\mathrm{2}}{\mathrm{3}}×\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{5}+\frac{\pi}{\:\sqrt{\mathrm{5}}}.. \\ $$$$ \\ $$$$ \\ $$
Answered by phanphuoc last updated on 30/Aug/21
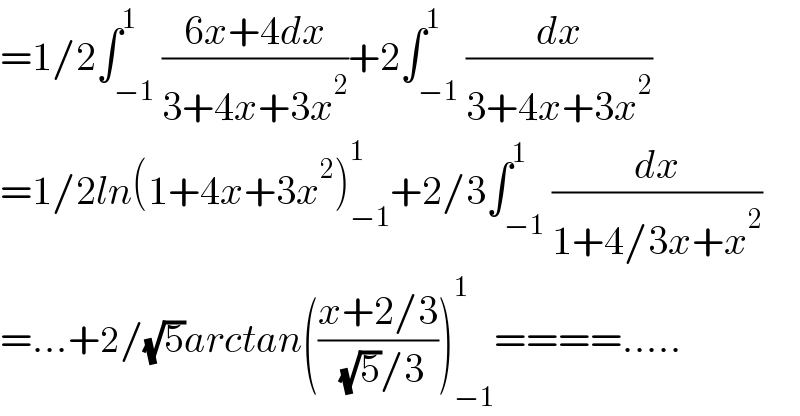
$$=\mathrm{1}/\mathrm{2}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{6}{x}+\mathrm{4}{dx}}{\mathrm{3}+\mathrm{4}{x}+\mathrm{3}{x}^{\mathrm{2}} }+\mathrm{2}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{3}+\mathrm{4}{x}+\mathrm{3}{x}^{\mathrm{2}} } \\ $$$$=\mathrm{1}/\mathrm{2}{ln}\left(\mathrm{1}+\mathrm{4}{x}+\mathrm{3}{x}^{\mathrm{2}} \right)_{−\mathrm{1}} ^{\mathrm{1}} +\mathrm{2}/\mathrm{3}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+\mathrm{4}/\mathrm{3}{x}+{x}^{\mathrm{2}} } \\ $$$$=…+\mathrm{2}/\sqrt{\mathrm{5}}{arctan}\left(\frac{{x}+\mathrm{2}/\mathrm{3}}{\:\sqrt{\mathrm{5}}/\mathrm{3}}\right)_{−\mathrm{1}} ^{\mathrm{1}} ====….. \\ $$
