Question Number 91452 by M±th+et+s last updated on 30/Apr/20

$$\:\:\:\sqrt[{\mathrm{4}}]{−\mathrm{1}}\:=? \\ $$
Commented by M±th+et+s last updated on 30/Apr/20
$${thanx}\:{for}\:{solutions}\: \\ $$
Answered by mr W last updated on 30/Apr/20
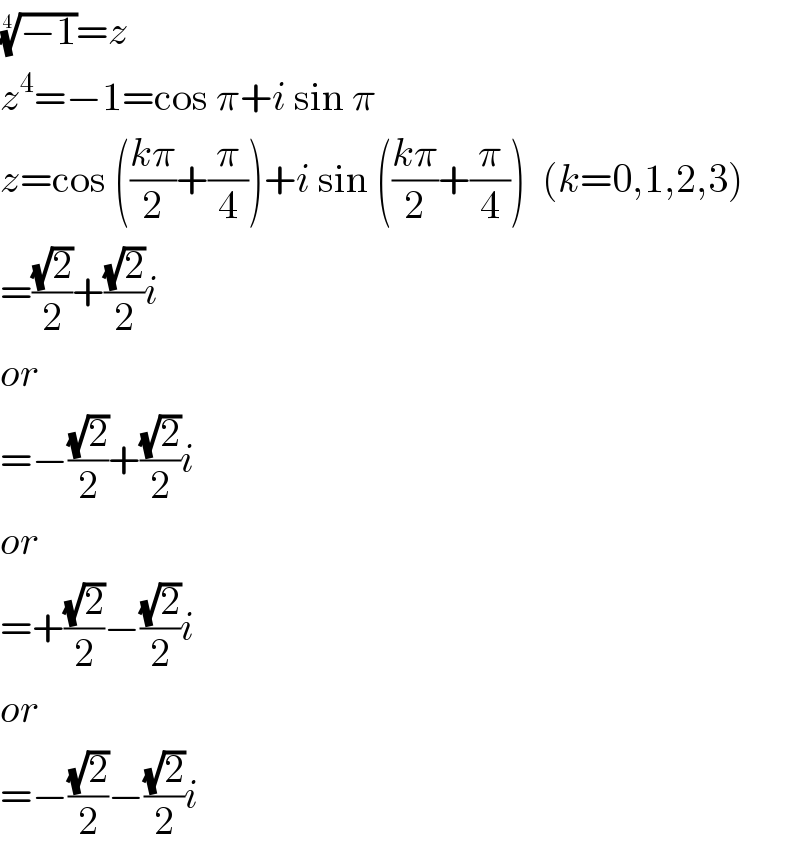
$$\sqrt[{\mathrm{4}}]{−\mathrm{1}}={z} \\ $$$${z}^{\mathrm{4}} =−\mathrm{1}=\mathrm{cos}\:\pi+{i}\:\mathrm{sin}\:\pi \\ $$$${z}=\mathrm{cos}\:\left(\frac{{k}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)+{i}\:\mathrm{sin}\:\left(\frac{{k}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\:\:\left({k}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3}\right) \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{i} \\ $$$${or} \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{i} \\ $$$${or} \\ $$$$=+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{i} \\ $$$${or} \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{i} \\ $$
Answered by MJS last updated on 30/Apr/20

$$−\mathrm{1}=\mathrm{e}^{\mathrm{i}\pi} \\ $$$$\sqrt[{\mathrm{4}}]{\mathrm{e}^{\mathrm{i}\pi} }=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{i} \\ $$
