Question Number 123650 by Dwaipayan Shikari last updated on 27/Nov/20
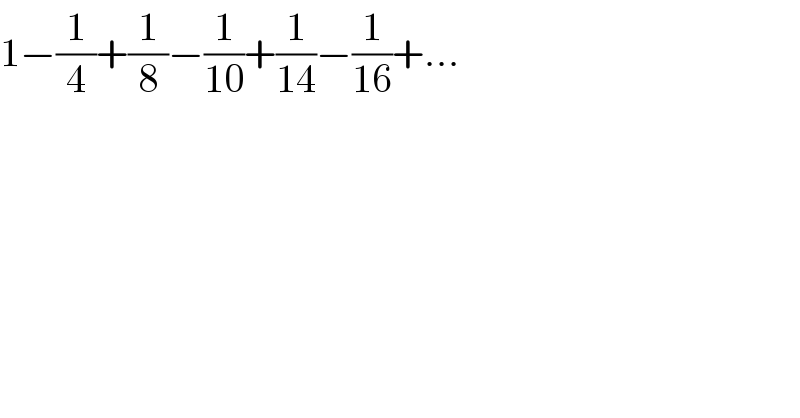
$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{14}}−\frac{\mathrm{1}}{\mathrm{16}}+… \\ $$
Commented by MJS_new last updated on 27/Nov/20

$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{misread}\:\mathrm{it}… \\ $$
Commented by Dwaipayan Shikari last updated on 27/Nov/20
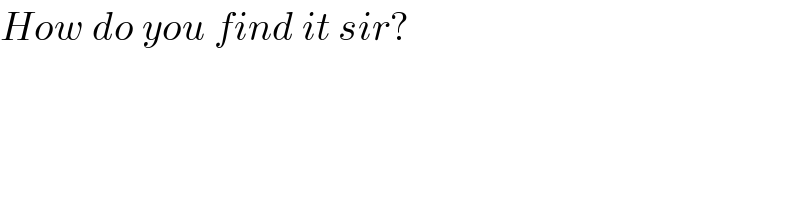
$${How}\:{do}\:{you}\:{find}\:{it}\:{sir}? \\ $$
Commented by MJS_new last updated on 27/Nov/20
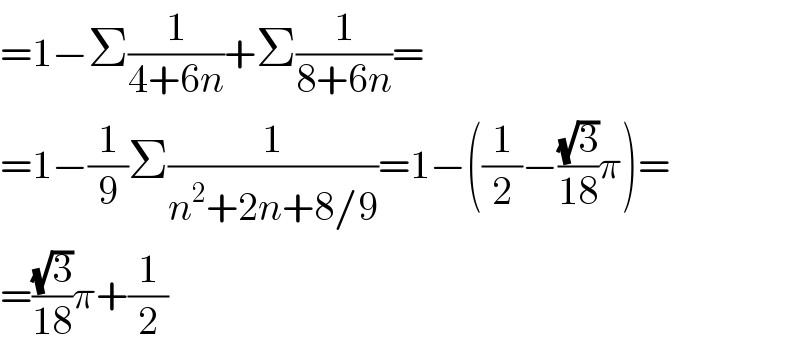
$$=\mathrm{1}−\Sigma\frac{\mathrm{1}}{\mathrm{4}+\mathrm{6}{n}}+\Sigma\frac{\mathrm{1}}{\mathrm{8}+\mathrm{6}{n}}= \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{9}}\Sigma\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{8}/\mathrm{9}}=\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\pi\right)= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\pi+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Nov/20
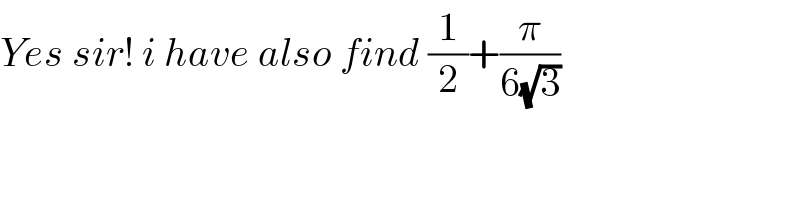
$${Yes}\:{sir}!\:{i}\:{have}\:{also}\:{find}\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}} \\ $$
