Question Number 120984 by pooooop last updated on 04/Nov/20
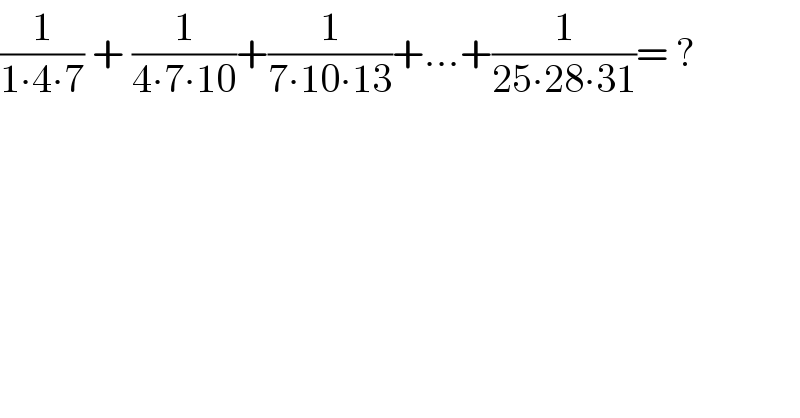
$$\frac{\mathrm{1}}{\mathrm{1}\centerdot\mathrm{4}\centerdot\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{4}\centerdot\mathrm{7}\centerdot\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{7}\centerdot\mathrm{10}\centerdot\mathrm{13}}+…+\frac{\mathrm{1}}{\mathrm{25}\centerdot\mathrm{28}\centerdot\mathrm{31}}=\:? \\ $$
Answered by Dwaipayan Shikari last updated on 04/Nov/20
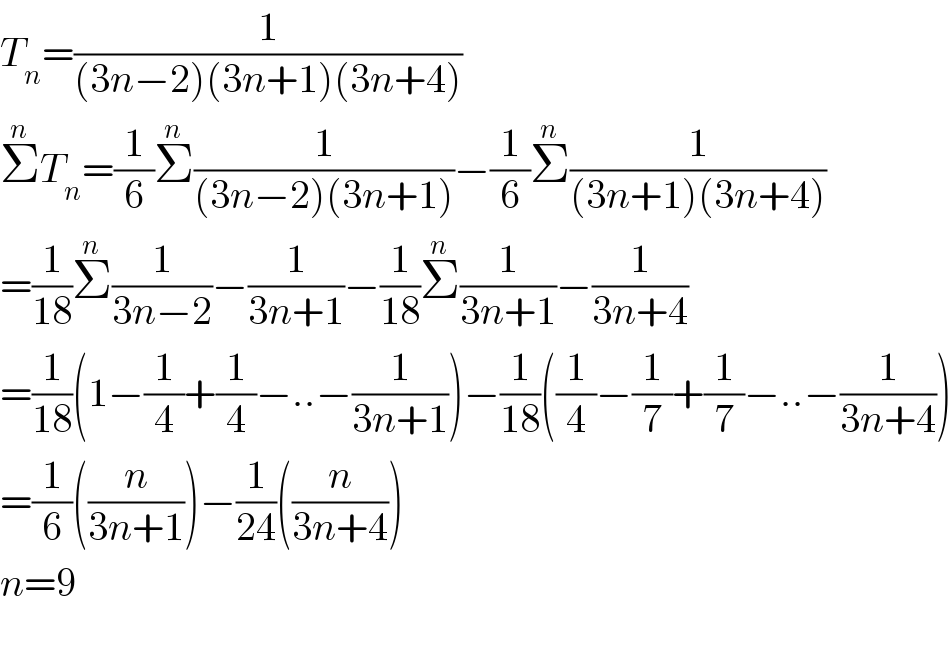
$${T}_{{n}} =\frac{\mathrm{1}}{\left(\mathrm{3}{n}−\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{4}\right)} \\ $$$$\overset{{n}} {\sum}{T}_{{n}} =\frac{\mathrm{1}}{\mathrm{6}}\overset{{n}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}−\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{6}}\overset{{n}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{4}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{18}}\overset{{n}} {\sum}\frac{\mathrm{1}}{\mathrm{3}{n}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{18}}\overset{{n}} {\sum}\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{18}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}−..−\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{18}}\left(\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{7}}−..−\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{{n}}{\mathrm{3}{n}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{24}}\left(\frac{{n}}{\mathrm{3}{n}+\mathrm{4}}\right) \\ $$$${n}=\mathrm{9} \\ $$$$ \\ $$
Commented by pooooop last updated on 04/Nov/20

$${n}=\mathrm{25}\:????? \\ $$
Commented by pooooop last updated on 04/Nov/20

$$\mathrm{3}\boldsymbol{{n}}−\mathrm{2}=\mathrm{25} \\ $$$$\boldsymbol{{n}}=\mathrm{9} \\ $$
Answered by TANMAY PANACEA last updated on 04/Nov/20
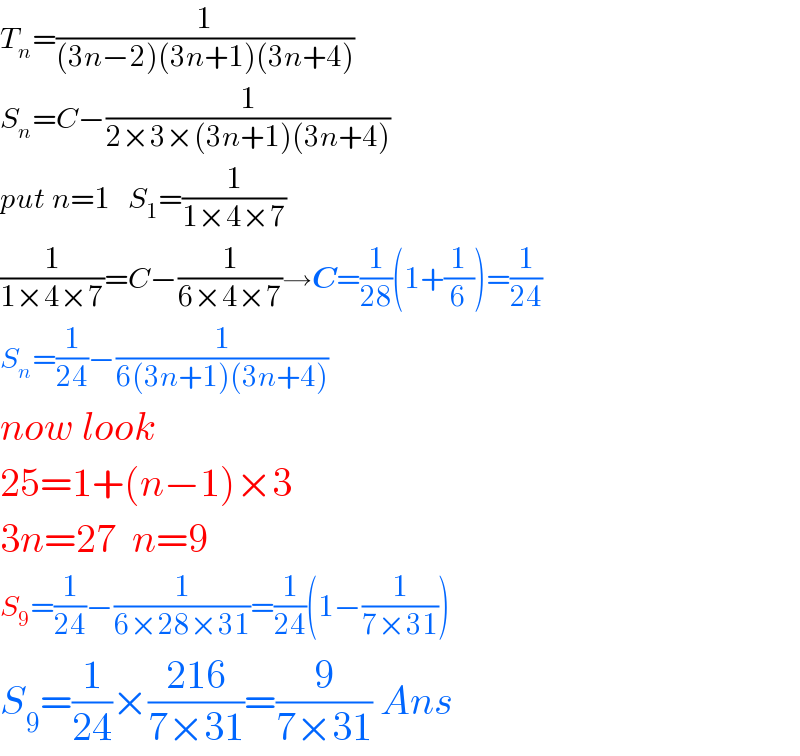
$${T}_{{n}} =\frac{\mathrm{1}}{\left(\mathrm{3}{n}−\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{4}\right)} \\ $$$${S}_{{n}} ={C}−\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}×\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{4}\right)} \\ $$$${put}\:{n}=\mathrm{1}\:\:\:{S}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}×\mathrm{4}×\mathrm{7}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}×\mathrm{4}×\mathrm{7}}={C}−\frac{\mathrm{1}}{\mathrm{6}×\mathrm{4}×\mathrm{7}}\rightarrow\boldsymbol{{C}}=\frac{\mathrm{1}}{\mathrm{28}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\right)=\frac{\mathrm{1}}{\mathrm{24}} \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{24}}−\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{4}\right)} \\ $$$${now}\:{look} \\ $$$$\mathrm{25}=\mathrm{1}+\left({n}−\mathrm{1}\right)×\mathrm{3} \\ $$$$\mathrm{3}{n}=\mathrm{27}\:\:{n}=\mathrm{9} \\ $$$${S}_{\mathrm{9}} =\frac{\mathrm{1}}{\mathrm{24}}−\frac{\mathrm{1}}{\mathrm{6}×\mathrm{28}×\mathrm{31}}=\frac{\mathrm{1}}{\mathrm{24}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{7}×\mathrm{31}}\right) \\ $$$${S}_{\mathrm{9}} =\frac{\mathrm{1}}{\mathrm{24}}×\frac{\mathrm{216}}{\mathrm{7}×\mathrm{31}}=\frac{\mathrm{9}}{\mathrm{7}×\mathrm{31}}\:{Ans} \\ $$
Commented by pooooop last updated on 04/Nov/20

$$\:\:\boldsymbol{{thank}}\:\:\boldsymbol{{you}}\:\:!!! \\ $$
Commented by TANMAY PANACEA last updated on 04/Nov/20

$${most}\:{welcome} \\ $$
