Question Number 122518 by Dwaipayan Shikari last updated on 17/Nov/20
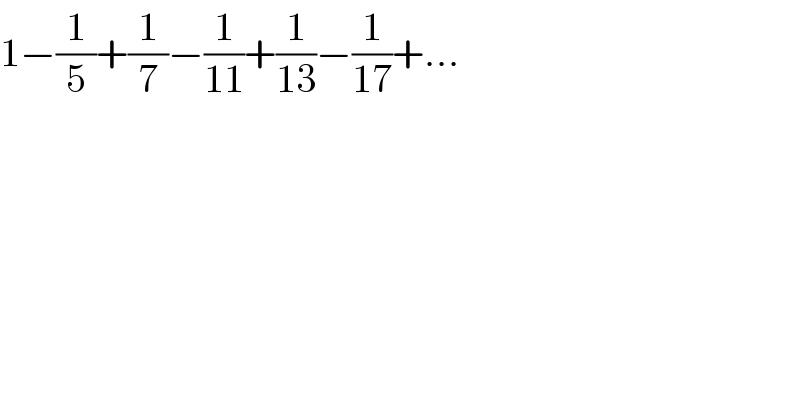
$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{11}}+\frac{\mathrm{1}}{\mathrm{13}}−\frac{\mathrm{1}}{\mathrm{17}}+… \\ $$
Commented by Dwaipayan Shikari last updated on 17/Nov/20
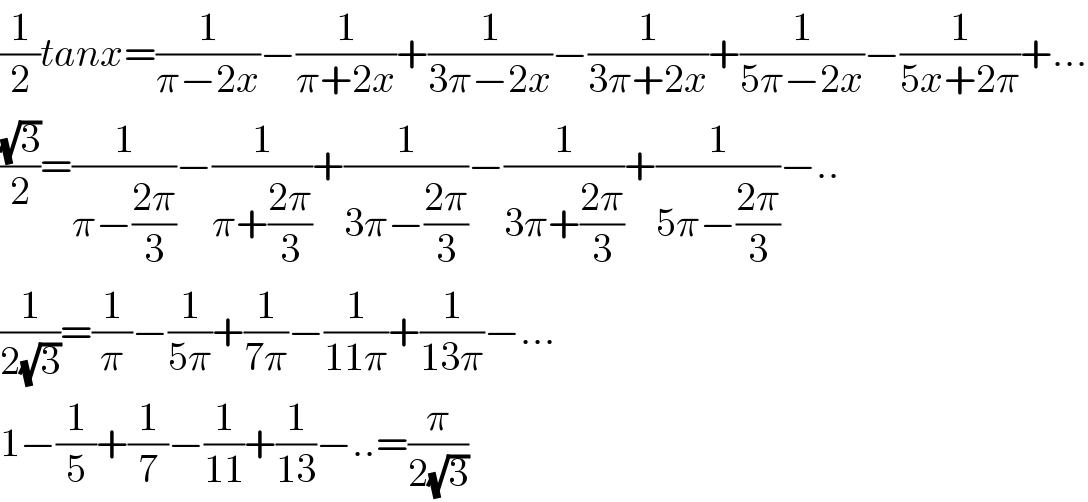
$$\frac{\mathrm{1}}{\mathrm{2}}{tanx}=\frac{\mathrm{1}}{\pi−\mathrm{2}{x}}−\frac{\mathrm{1}}{\pi+\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{3}\pi−\mathrm{2}{x}}−\frac{\mathrm{1}}{\mathrm{3}\pi+\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{5}\pi−\mathrm{2}{x}}−\frac{\mathrm{1}}{\mathrm{5}{x}+\mathrm{2}\pi}+… \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{1}}{\pi−\frac{\mathrm{2}\pi}{\mathrm{3}}}−\frac{\mathrm{1}}{\pi+\frac{\mathrm{2}\pi}{\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{3}\pi−\frac{\mathrm{2}\pi}{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{3}\pi+\frac{\mathrm{2}\pi}{\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{5}\pi−\frac{\mathrm{2}\pi}{\mathrm{3}}}−.. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}=\frac{\mathrm{1}}{\pi}−\frac{\mathrm{1}}{\mathrm{5}\pi}+\frac{\mathrm{1}}{\mathrm{7}\pi}−\frac{\mathrm{1}}{\mathrm{11}\pi}+\frac{\mathrm{1}}{\mathrm{13}\pi}−… \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{11}}+\frac{\mathrm{1}}{\mathrm{13}}−..=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$
Answered by mnjuly1970 last updated on 18/Nov/20
![S=1+(1/6)Σ_(n=1) ^∞ (1/((n+(1/6)))) −(1/6)Σ_(n=1) ^∞ (1/((n−(1/6)))) =1+(1/6)[ψ((5/6))−ψ((7/6))] =1+(1/6)[ψ((5/6))−ψ((1/6))−6] =(1/6)[ψ(1−(1/6))−ψ((1/6))] =(1/6)(πcot((π/6)))=(π/6)∗(√3)=(π/(2(√3))) ✓](https://www.tinkutara.com/question/Q122596.png)
$$\:{S}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{6}}\right)}\:−\frac{\mathrm{1}}{\mathrm{6}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−\frac{\mathrm{1}}{\mathrm{6}}\right)} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\left[\psi\left(\frac{\mathrm{5}}{\mathrm{6}}\right)−\psi\left(\frac{\mathrm{7}}{\mathrm{6}}\right)\right] \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\left[\psi\left(\frac{\mathrm{5}}{\mathrm{6}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{6}}\right)−\mathrm{6}\right] \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{6}}\left[\psi\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\right] \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{6}}\left(\pi{cot}\left(\frac{\pi}{\mathrm{6}}\right)\right)=\frac{\pi}{\mathrm{6}}\ast\sqrt{\mathrm{3}}=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Dwaipayan Shikari last updated on 18/Nov/20
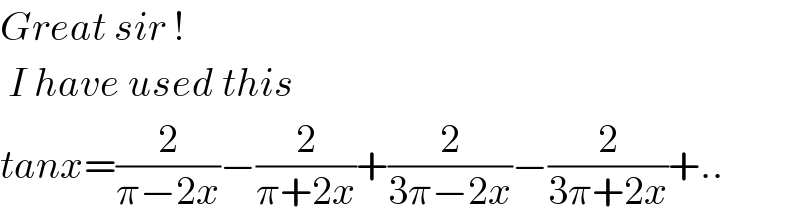
$${Great}\:{sir}\:! \\ $$$$\:{I}\:{have}\:{used}\:{this}\: \\ $$$${tanx}=\frac{\mathrm{2}}{\pi−\mathrm{2}{x}}−\frac{\mathrm{2}}{\pi+\mathrm{2}{x}}+\frac{\mathrm{2}}{\mathrm{3}\pi−\mathrm{2}{x}}−\frac{\mathrm{2}}{\mathrm{3}\pi+\mathrm{2}{x}}+.. \\ $$
Commented by mnjuly1970 last updated on 18/Nov/20
$${extraordinary}\:{sir}\:{dwaipayan} \\ $$
