Question Number 106860 by Dwaipayan Shikari last updated on 07/Aug/20
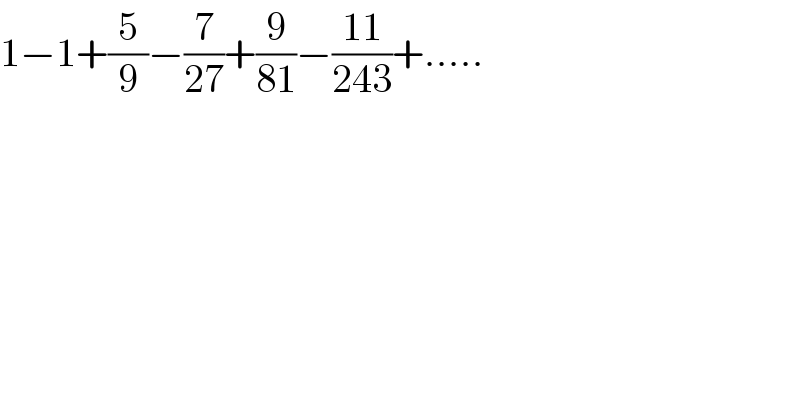
$$\mathrm{1}−\mathrm{1}+\frac{\mathrm{5}}{\mathrm{9}}−\frac{\mathrm{7}}{\mathrm{27}}+\frac{\mathrm{9}}{\mathrm{81}}−\frac{\mathrm{11}}{\mathrm{243}}+….. \\ $$
Commented by Dwaipayan Shikari last updated on 07/Aug/20
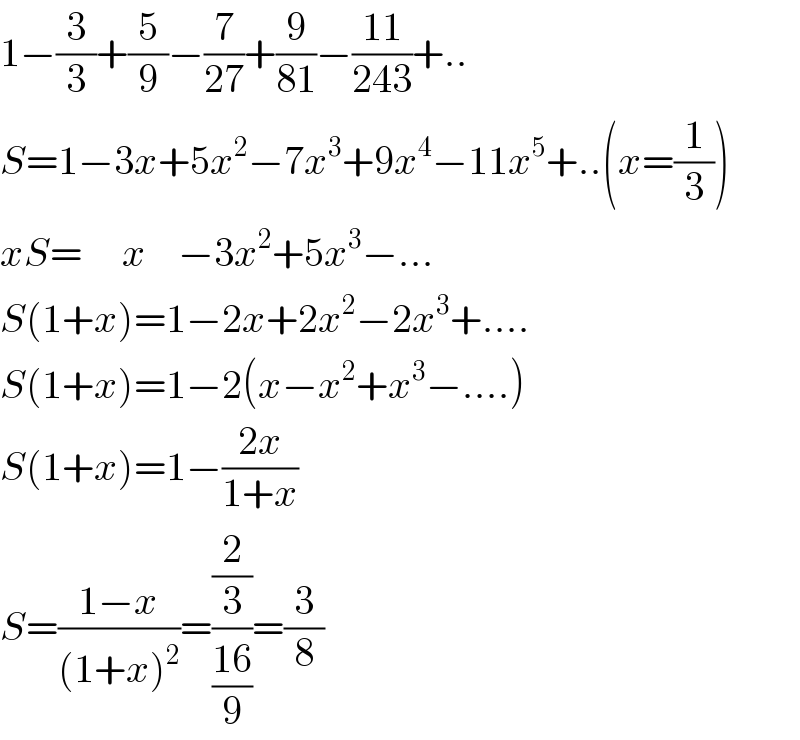
$$\mathrm{1}−\frac{\mathrm{3}}{\mathrm{3}}+\frac{\mathrm{5}}{\mathrm{9}}−\frac{\mathrm{7}}{\mathrm{27}}+\frac{\mathrm{9}}{\mathrm{81}}−\frac{\mathrm{11}}{\mathrm{243}}+.. \\ $$$${S}=\mathrm{1}−\mathrm{3}{x}+\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{4}} −\mathrm{11}{x}^{\mathrm{5}} +..\left({x}=\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${xS}=\:\:\:\:\:{x}\:\:\:\:−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{5}{x}^{\mathrm{3}} −… \\ $$$${S}\left(\mathrm{1}+{x}\right)=\mathrm{1}−\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{3}} +…. \\ $$$${S}\left(\mathrm{1}+{x}\right)=\mathrm{1}−\mathrm{2}\left({x}−{x}^{\mathrm{2}} +{x}^{\mathrm{3}} −….\right) \\ $$$${S}\left(\mathrm{1}+{x}\right)=\mathrm{1}−\frac{\mathrm{2}{x}}{\mathrm{1}+{x}} \\ $$$${S}=\frac{\mathrm{1}−{x}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\frac{\frac{\mathrm{2}}{\mathrm{3}}}{\frac{\mathrm{16}}{\mathrm{9}}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$
Commented by bemath last updated on 07/Aug/20

$$\mathrm{cooll} \\ $$
Commented by abdomathmax last updated on 07/Aug/20
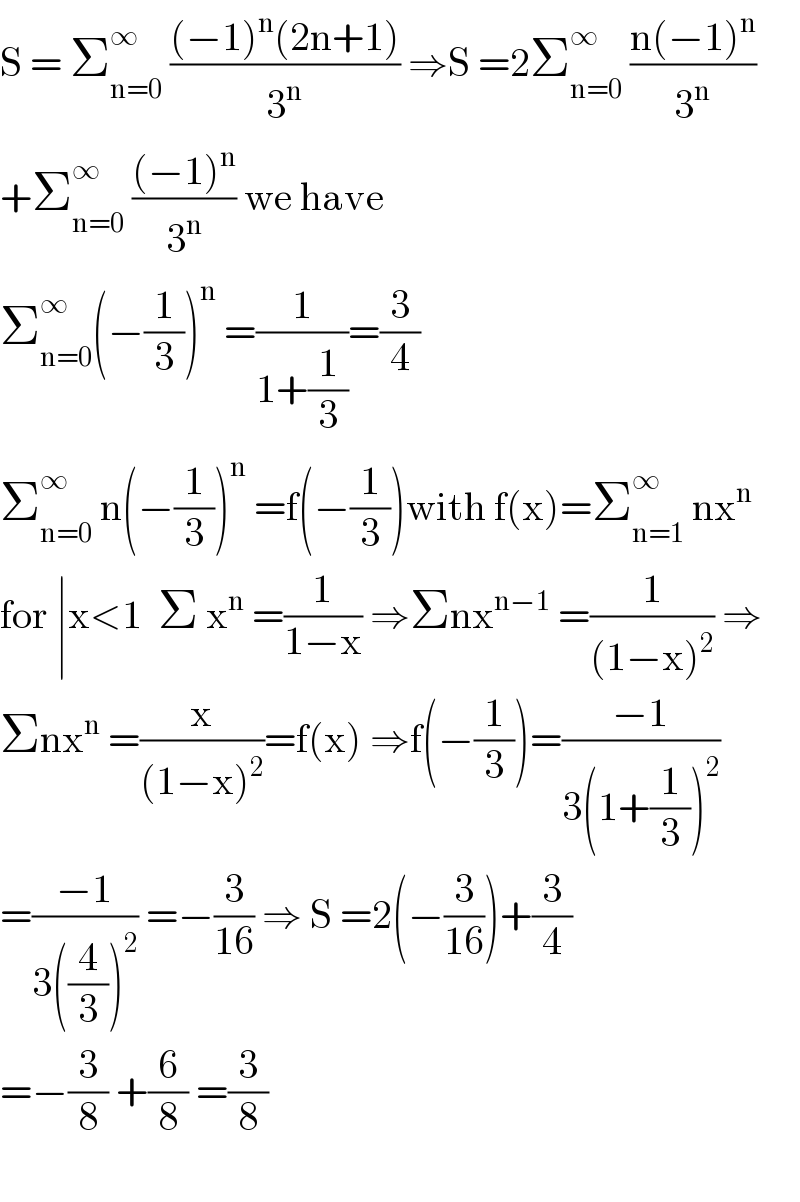
$$\mathrm{S}\:=\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{3}^{\mathrm{n}} }\:\Rightarrow\mathrm{S}\:=\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}} } \\ $$$$+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}} }\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{n}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{n}} \:=\mathrm{f}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)\mathrm{with}\:\mathrm{f}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}} \\ $$$$\mathrm{for}\:\mid\mathrm{x}<\mathrm{1}\:\:\Sigma\:\mathrm{x}^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow\Sigma\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\Sigma\mathrm{nx}^{\mathrm{n}} \:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }=\mathrm{f}\left(\mathrm{x}\right)\:\Rightarrow\mathrm{f}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{−\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{1}}{\mathrm{3}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} }\:=−\frac{\mathrm{3}}{\mathrm{16}}\:\Rightarrow\:\mathrm{S}\:=\mathrm{2}\left(−\frac{\mathrm{3}}{\mathrm{16}}\right)+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{8}}\:+\frac{\mathrm{6}}{\mathrm{8}}\:=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$ \\ $$
