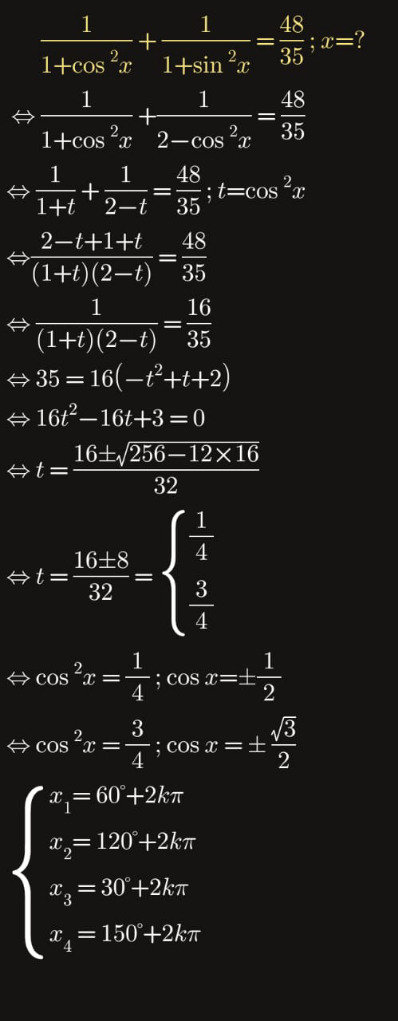Question Number 169771 by greougoury555 last updated on 08/May/22

$$\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}\:+\:\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{1}}\:=\:\frac{\mathrm{48}}{\mathrm{35}} \\ $$
Answered by kapoorshah last updated on 08/May/22

$${SyberMath} \\ $$
Answered by thfchristopher last updated on 08/May/22

$$\Rightarrow\frac{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{1}+\mathrm{cos}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{2}} {x}\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{cos}^{\mathrm{2}} {x}}=\frac{\mathrm{48}}{\mathrm{35}} \\ $$$$\Rightarrow\frac{\mathrm{3}}{\mathrm{2}+\mathrm{sin}^{\mathrm{2}} {x}\mathrm{cos}^{\mathrm{2}} {x}}=\frac{\mathrm{48}}{\mathrm{35}} \\ $$$$\Rightarrow\mathrm{105}=\mathrm{96}+\mathrm{48sin}^{\mathrm{2}} {x}\mathrm{cos}^{\mathrm{2}} {x} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} {x}\mathrm{cos}^{\mathrm{2}} {x}=\frac{\mathrm{9}}{\mathrm{48}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}=\frac{\mathrm{9}}{\mathrm{48}} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}=\frac{\mathrm{36}}{\mathrm{48}} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:\:\:\mathrm{or}\:\:\:\:\mathrm{sin}\:\mathrm{2}{x}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{2}{x}={n}\pi\mp\frac{\pi}{\mathrm{3}} \\ $$$${x}=\frac{{n}\pi}{\mathrm{2}}\mp\frac{\pi}{\mathrm{6}} \\ $$
Answered by cortano1 last updated on 08/May/22