Question Number 129404 by bemath last updated on 15/Jan/21
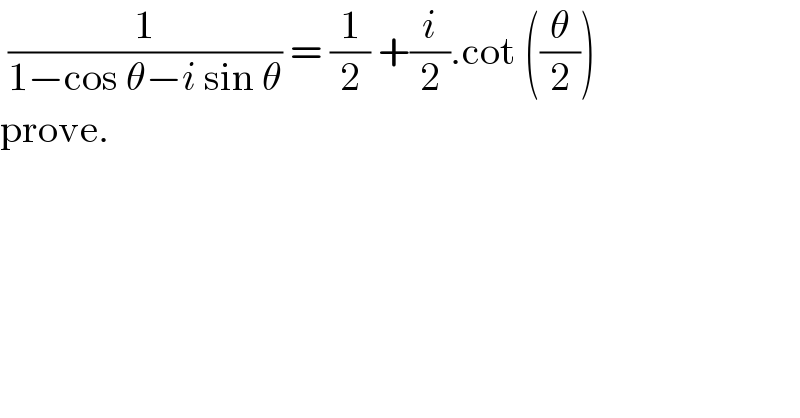
$$\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{cos}\:\theta−{i}\:\mathrm{sin}\:\theta}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{{i}}{\mathrm{2}}.\mathrm{cot}\:\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$$\mathrm{prove}. \\ $$
Answered by MJS_new last updated on 15/Jan/21
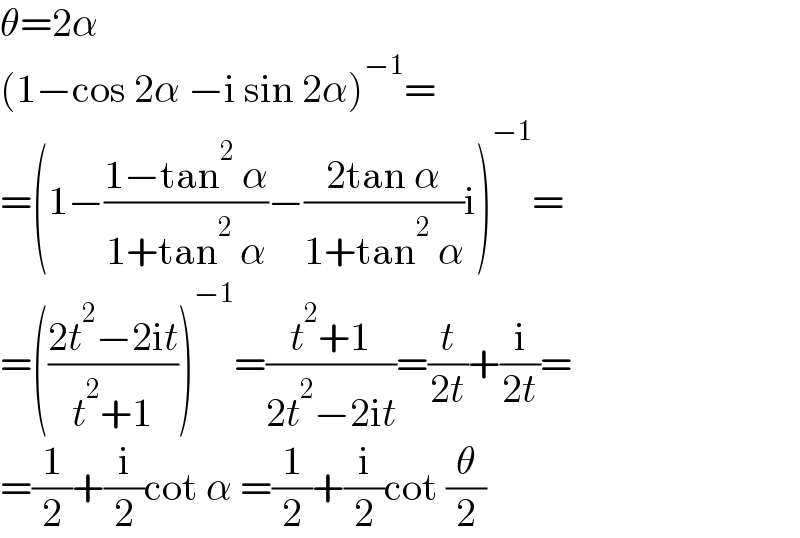
$$\theta=\mathrm{2}\alpha \\ $$$$\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\alpha\:−\mathrm{i}\:\mathrm{sin}\:\mathrm{2}\alpha\right)^{−\mathrm{1}} = \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\alpha}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}−\frac{\mathrm{2tan}\:\alpha}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}\mathrm{i}\right)^{−\mathrm{1}} = \\ $$$$=\left(\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2i}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\right)^{−\mathrm{1}} =\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2i}{t}}=\frac{{t}}{\mathrm{2}{t}}+\frac{\mathrm{i}}{\mathrm{2}{t}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}}{\mathrm{2}}\mathrm{cot}\:\alpha\:=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}}{\mathrm{2}}\mathrm{cot}\:\frac{\theta}{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 16/Jan/21

$$\mathrm{yes} \\ $$
Commented by liberty last updated on 16/Jan/21

$$\mathrm{t}\:=\:\mathrm{tan}\:\alpha? \\ $$
Answered by physicstutes last updated on 15/Jan/21
![((1/(1−cos θ−isin θ)))(((1−cos θ + i sin θ)/(1−cos θ+isin θ))) = ((1−cos θ + isin θ)/((1−cos θ)^2 +(sin θ)^2 )) = ((1−cos θ + isin θ)/(1−2cos θ + cos^2 θ+sin^2 θ)) = ((1−cos θ + isin θ)/(2−2cos θ)) = (1/2)[((1−(1−2sin^2 (θ/2)) + i 2sin(θ/2)cos(θ/2))/(1−(1−2sin^2 (θ/2))))] = (1/2)[1 + icot (θ/2)]= (1/2) + (i/2) cot ((θ/2))](https://www.tinkutara.com/question/Q129439.png)
$$\:\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{cos}\:\theta−{i}\mathrm{sin}\:\theta}\right)\left(\frac{\mathrm{1}−\mathrm{cos}\:\theta\:+\:{i}\:\mathrm{sin}\:\theta}{\mathrm{1}−\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta}\right)\:=\:\frac{\mathrm{1}−\mathrm{cos}\:\theta\:+\:{i}\mathrm{sin}\:\theta}{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left(\mathrm{sin}\:\theta\right)^{\mathrm{2}} }\: \\ $$$$\:=\:\frac{\mathrm{1}−\mathrm{cos}\:\theta\:+\:{i}\mathrm{sin}\:\theta}{\mathrm{1}−\mathrm{2cos}\:\theta\:+\:\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta}\:=\:\frac{\mathrm{1}−\mathrm{cos}\:\theta\:+\:{i}\mathrm{sin}\:\theta}{\mathrm{2}−\mathrm{2cos}\:\theta}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\right)\:+\:{i}\:\mathrm{2sin}\frac{\theta}{\mathrm{2}}\mathrm{cos}\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\right)}\right] \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}\:+\:{i}\mathrm{cot}\:\frac{\theta}{\mathrm{2}}\right]=\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{{i}}{\mathrm{2}}\:\mathrm{cot}\:\left(\frac{\theta}{\mathrm{2}}\right)\: \\ $$$$ \\ $$
