Question Number 105455 by john santu last updated on 29/Jul/20
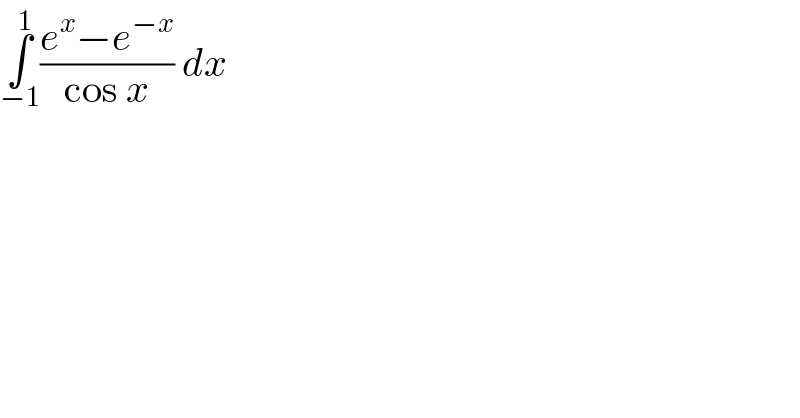
$$\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{cos}\:{x}}\:{dx}\: \\ $$
Answered by 1549442205PVT last updated on 29/Jul/20
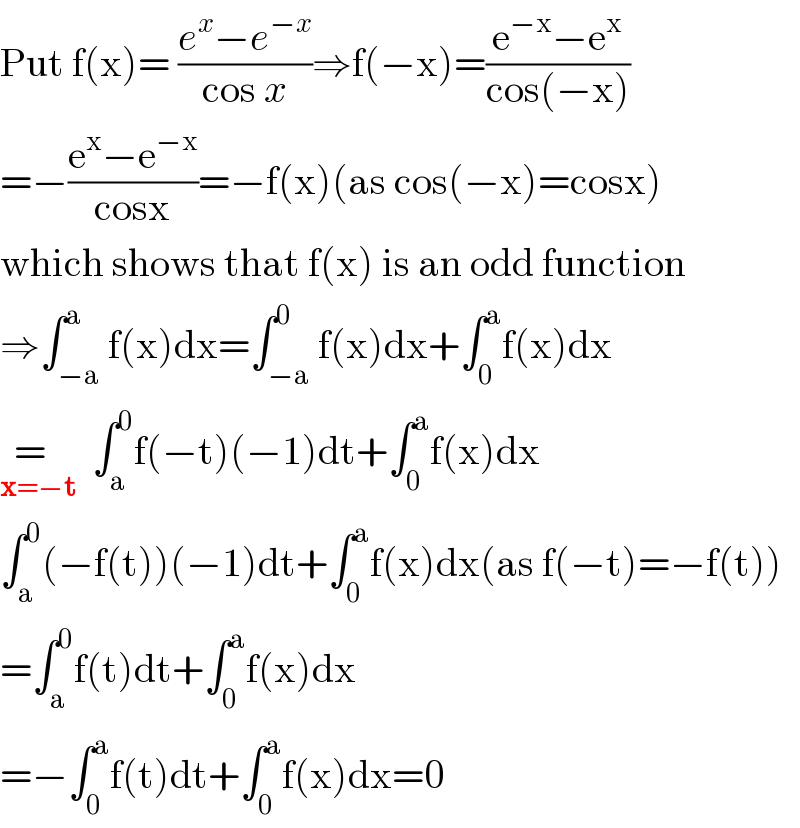
$$\mathrm{Put}\:\mathrm{f}\left(\mathrm{x}\right)=\:\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{cos}\:{x}}\Rightarrow\mathrm{f}\left(−\mathrm{x}\right)=\frac{\mathrm{e}^{−\mathrm{x}} −\mathrm{e}^{\mathrm{x}} }{\mathrm{cos}\left(−\mathrm{x}\right)} \\ $$$$=−\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{cosx}}=−\mathrm{f}\left(\mathrm{x}\right)\left(\mathrm{as}\:\mathrm{cos}\left(−\mathrm{x}\right)=\mathrm{cosx}\right) \\ $$$$\mathrm{which}\:\mathrm{shows}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{function} \\ $$$$\Rightarrow\int_{−\mathrm{a}} ^{\mathrm{a}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\int_{−\mathrm{a}} ^{\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{a}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\underset{\boldsymbol{\mathrm{x}}=−\boldsymbol{\mathrm{t}}} {=\:\:}\:\:\int_{\mathrm{a}} ^{\mathrm{0}} \mathrm{f}\left(−\mathrm{t}\right)\left(−\mathrm{1}\right)\mathrm{dt}+\int_{\mathrm{0}} ^{\mathrm{a}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\int_{\mathrm{a}} ^{\mathrm{0}} \left(−\mathrm{f}\left(\mathrm{t}\right)\right)\left(−\mathrm{1}\right)\mathrm{dt}+\int_{\mathrm{0}} ^{\mathrm{a}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\left(\mathrm{as}\:\mathrm{f}\left(−\mathrm{t}\right)=−\mathrm{f}\left(\mathrm{t}\right)\right) \\ $$$$=\int_{\mathrm{a}} ^{\mathrm{0}} \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}+\int_{\mathrm{0}} ^{\mathrm{a}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{a}} \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}+\int_{\mathrm{0}} ^{\mathrm{a}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{0} \\ $$
Answered by Dwaipayan Shikari last updated on 29/Jul/20
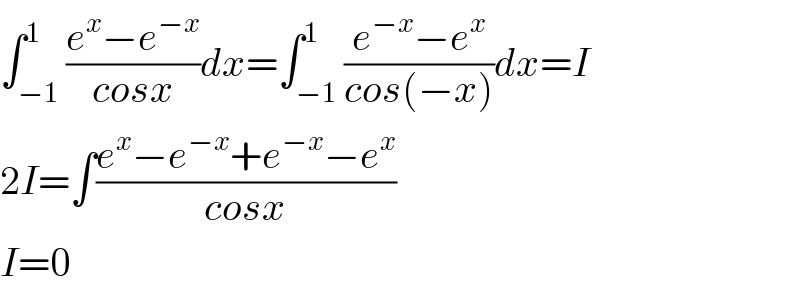
$$\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{e}^{{x}} −{e}^{−{x}} }{{cosx}}{dx}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{e}^{−{x}} −{e}^{{x}} }{{cos}\left(−{x}\right)}{dx}={I} \\ $$$$\mathrm{2}{I}=\int\frac{{e}^{{x}} −{e}^{−{x}} +{e}^{−{x}} −{e}^{{x}} }{{cosx}} \\ $$$${I}=\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 29/Jul/20
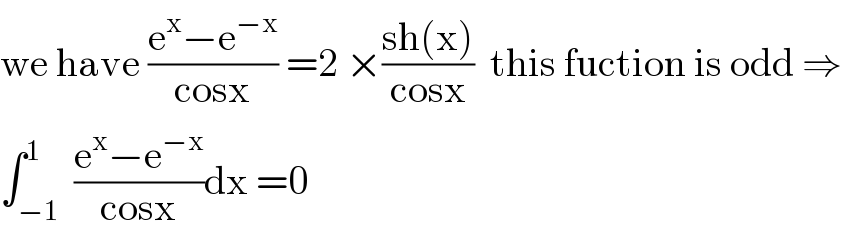
$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{cosx}}\:=\mathrm{2}\:×\frac{\mathrm{sh}\left(\mathrm{x}\right)}{\mathrm{cosx}}\:\:\mathrm{this}\:\mathrm{fuction}\:\mathrm{is}\:\mathrm{odd}\:\Rightarrow \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{cosx}}\mathrm{dx}\:=\mathrm{0} \\ $$
