Question Number 44921 by manish09@gmail.com last updated on 06/Oct/18

$$\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{ln}\:\mathrm{x}}=? \\ $$
Commented by MJS last updated on 06/Oct/18

$$\mathrm{see}\:\mathrm{question}\:\mathrm{44674} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Oct/18
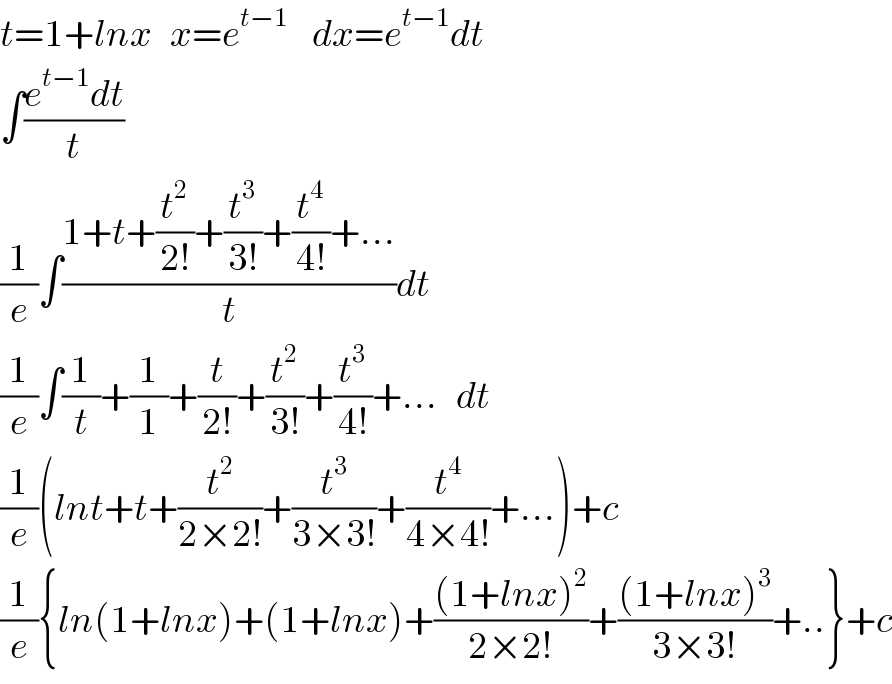
$${t}=\mathrm{1}+{lnx}\:\:\:{x}={e}^{{t}−\mathrm{1}} \:\:\:\:{dx}={e}^{{t}−\mathrm{1}} {dt} \\ $$$$\int\frac{{e}^{{t}−\mathrm{1}} {dt}}{{t}} \\ $$$$\frac{\mathrm{1}}{{e}}\int\frac{\mathrm{1}+{t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{t}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{t}^{\mathrm{4}} }{\mathrm{4}!}+…}{{t}}{dt} \\ $$$$\frac{\mathrm{1}}{{e}}\int\frac{\mathrm{1}}{{t}}+\frac{\mathrm{1}}{\mathrm{1}}+\frac{{t}}{\mathrm{2}!}+\frac{{t}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{t}^{\mathrm{3}} }{\mathrm{4}!}+…\:\:\:{dt} \\ $$$$\frac{\mathrm{1}}{{e}}\left({lnt}+{t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}!}+\frac{{t}^{\mathrm{3}} }{\mathrm{3}×\mathrm{3}!}+\frac{{t}^{\mathrm{4}} }{\mathrm{4}×\mathrm{4}!}+…\right)+{c} \\ $$$$\frac{\mathrm{1}}{{e}}\left\{{ln}\left(\mathrm{1}+{lnx}\right)+\left(\mathrm{1}+{lnx}\right)+\frac{\left(\mathrm{1}+{lnx}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}!}+\frac{\left(\mathrm{1}+{lnx}\right)^{\mathrm{3}} }{\mathrm{3}×\mathrm{3}!}+..\right\}+{c} \\ $$
Commented by arvinddayama01@gmail.com last updated on 07/Oct/18

$$\mathrm{Thanks} \\ $$
Commented by manish09@gmail.com last updated on 07/Oct/18

$$\mathrm{thanx}\:\:\:\mathrm{sir} \\ $$
