Menu Close

1-1-tanx-dx-

Tinku Tara 0 Comments
Pin




Question Number 42407 by Tawa1 last updated on 25/Aug/18
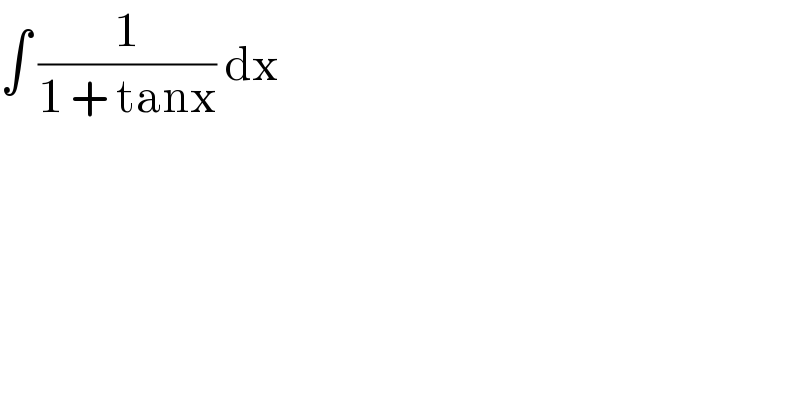
∫ (1/(1 + tanx)) dx
$$\int\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{tanx}}\:\mathrm{dx} \\ $$
Commented by maxmathsup by imad last updated on 25/Aug/18
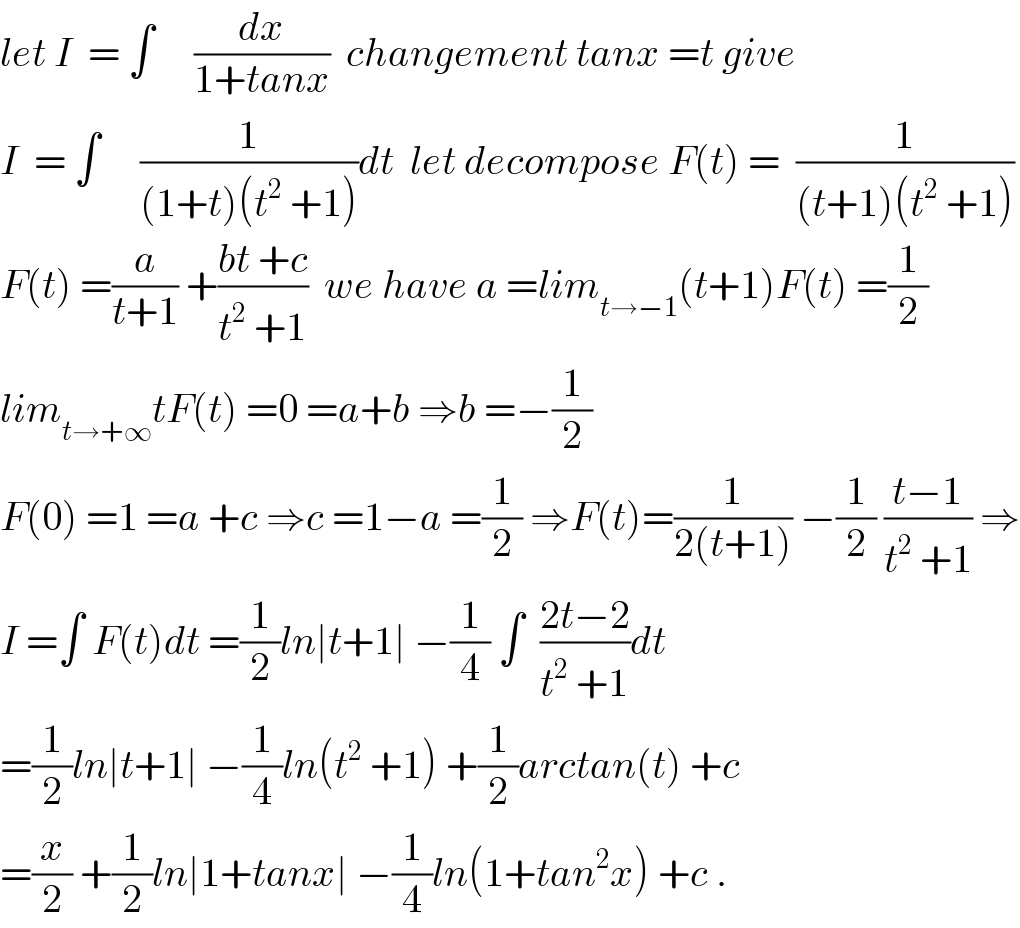
let I = ∫ (dx/(1+tanx)) changement tanx =t give I = ∫ (1/((1+t)(t^2 +1)))dt let decompose F(t) = (1/((t+1)(t^2 +1))) F(t) =(a/(t+1)) +((bt +c)/(t^2 +1)) we have a =lim_(t→−1) (t+1)F(t) =(1/2) lim_(t→+∞) tF(t) =0 =a+b ⇒b =−(1/2) F(0) =1 =a +c ⇒c =1−a =(1/2) ⇒F(t)=(1/(2(t+1))) −(1/2) ((t−1)/(t^2 +1)) ⇒ I =∫ F(t)dt =(1/2)ln∣t+1∣ −(1/4) ∫ ((2t−2)/(t^2 +1))dt =(1/2)ln∣t+1∣ −(1/4)ln(t^2 +1) +(1/2)arctan(t) +c =(x/2) +(1/2)ln∣1+tanx∣ −(1/4)ln(1+tan^2 x) +c .
$${let}\:{I}\:\:=\:\int\:\:\:\:\:\frac{{dx}}{\mathrm{1}+{tanx}}\:\:{changement}\:{tanx}\:={t}\:{give} \\ $$$${I}\:\:=\:\int\:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{dt}\:\:{let}\:{decompose}\:{F}\left({t}\right)\:=\:\:\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${F}\left({t}\right)\:=\frac{{a}}{{t}+\mathrm{1}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\:{we}\:{have}\:{a}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right){F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:={a}\:+{c}\:\Rightarrow{c}\:=\mathrm{1}−{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${I}\:=\int\:{F}\left({t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{t}+\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\:\frac{\mathrm{2}{t}−\mathrm{2}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{t}+\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left({t}\right)\:+{c} \\ $$$$=\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}+{tanx}\mid\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:+{c}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Aug/18
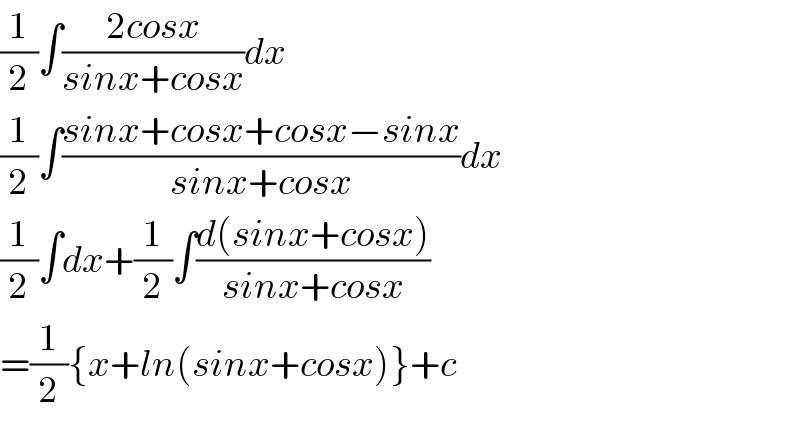
(1/2)∫((2cosx)/(sinx+cosx))dx (1/2)∫((sinx+cosx+cosx−sinx)/(sinx+cosx))dx (1/2)∫dx+(1/2)∫((d(sinx+cosx))/(sinx+cosx)) =(1/2){x+ln(sinx+cosx)}+c
$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{cosx}}{{sinx}+{cosx}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sinx}+{cosx}+{cosx}−{sinx}}{{sinx}+{cosx}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({sinx}+{cosx}\right)}{{sinx}+{cosx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{x}+{ln}\left({sinx}+{cosx}\right)\right\}+{c} \\ $$
Commented by Tawa1 last updated on 25/Aug/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *