Question Number 18396 by Joel577 last updated on 20/Jul/17

$$\int\:\sqrt{\mathrm{1}\:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }}\:\:{dx} \\ $$
Answered by b.e.h.i.8.3.417@gmail.com last updated on 20/Jul/17
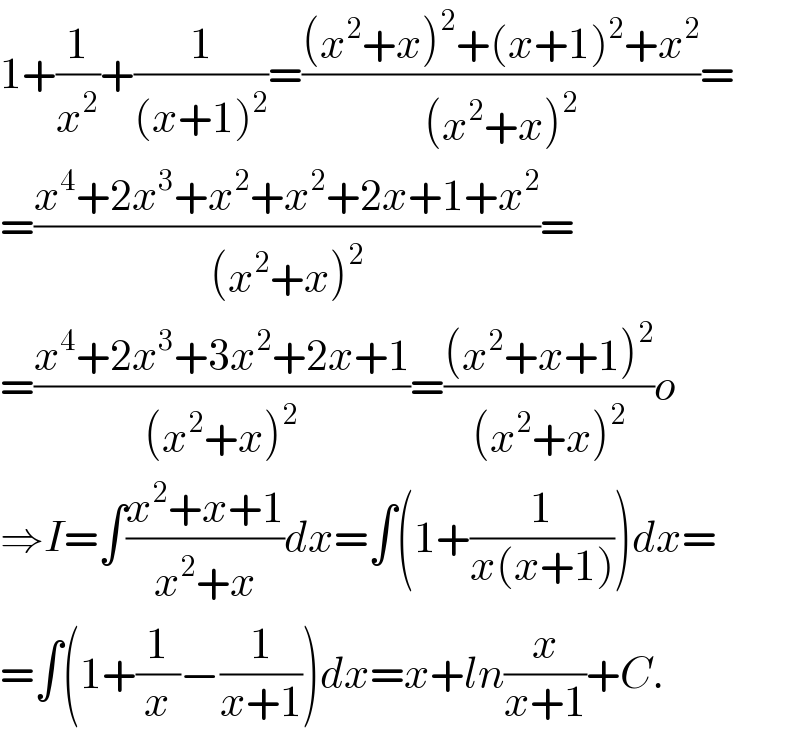
$$\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\left({x}^{\mathrm{2}} +{x}\right)^{\mathrm{2}} +\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{x}\right)^{\mathrm{2}} }= \\ $$$$=\frac{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}+{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{x}\right)^{\mathrm{2}} }= \\ $$$$=\frac{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}\right)^{\mathrm{2}} }=\frac{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{x}\right)^{\mathrm{2}} }{o} \\ $$$$\Rightarrow{I}=\int\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}}{dx}=\int\left(\mathrm{1}+\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)}\right){dx}= \\ $$$$=\int\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right){dx}={x}+{ln}\frac{{x}}{{x}+\mathrm{1}}+{C}. \\ $$
Commented by Joel577 last updated on 25/Jul/17

$${thank}\:{you}\:{very}\:{much} \\ $$
