1-1-x-2-4-1-x-2-1-

Question Number 104621 by ajfour last updated on 22/Jul/20

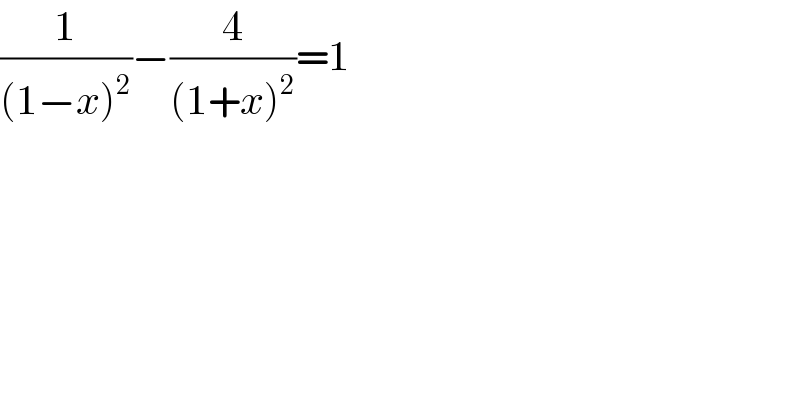
$$\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }−\frac{\mathrm{4}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\mathrm{1} \\ $$

Answered by prakash jain last updated on 22/Jul/20

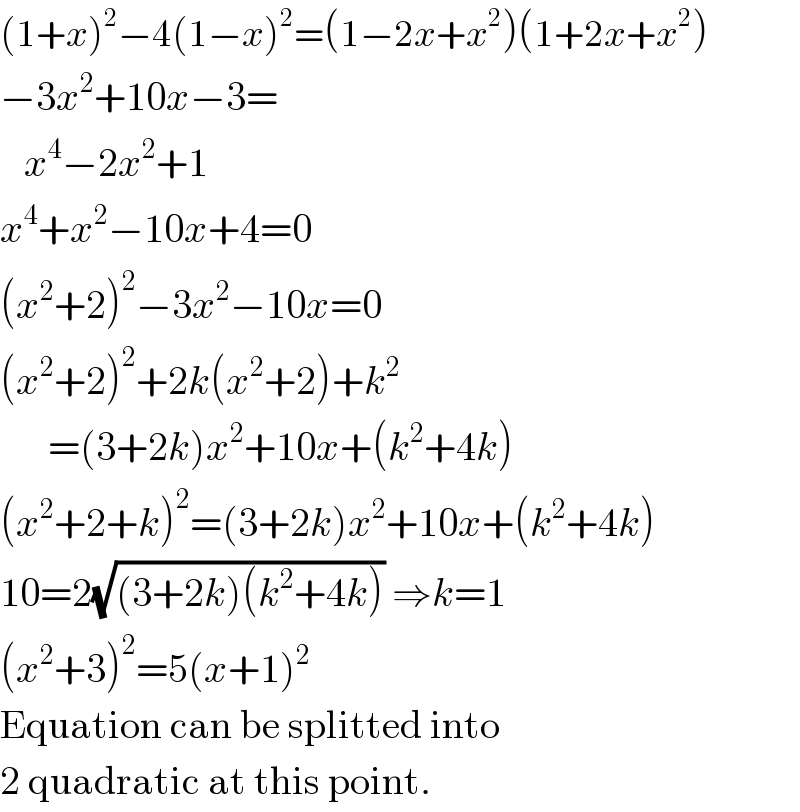
(1+x)^2 −4(1−x)^2 =(1−2x+x^2 )(1+2x+x^2 ) −3x^2 +10x−3= x^4 −2x^2 +1 x^4 +x^2 −10x+4=0 (x^2 +2)^2 −3x^2 −10x=0 (x^2 +2)^2 +2k(x^2 +2)+k^2 =(3+2k)x^2 +10x+(k^2 +4k) (x^2 +2+k)^2 =(3+2k)x^2 +10x+(k^2 +4k) 10=2(√((3+2k)(k^2 +4k))) ⇒k=1 (x^2 +3)^2 =5(x+1)^2 Equation can be splitted into 2 quadratic at this point.

$$\left(\mathrm{1}+{x}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{2}{x}+{x}^{\mathrm{2}} \right) \\ $$$$−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{10}{x}−\mathrm{3}= \\ $$$$\:\:\:{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{4}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{2}} −\mathrm{10}{x}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}{k}\left({x}^{\mathrm{2}} +\mathrm{2}\right)+{k}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\left(\mathrm{3}+\mathrm{2}{k}\right){x}^{\mathrm{2}} +\mathrm{10}{x}+\left({k}^{\mathrm{2}} +\mathrm{4}{k}\right) \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{2}+{k}\right)^{\mathrm{2}} =\left(\mathrm{3}+\mathrm{2}{k}\right){x}^{\mathrm{2}} +\mathrm{10}{x}+\left({k}^{\mathrm{2}} +\mathrm{4}{k}\right) \\ $$$$\mathrm{10}=\mathrm{2}\sqrt{\left(\mathrm{3}+\mathrm{2}{k}\right)\left({k}^{\mathrm{2}} +\mathrm{4}{k}\right)}\:\Rightarrow{k}=\mathrm{1} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} =\mathrm{5}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{Equation}\:\mathrm{can}\:\mathrm{be}\:\mathrm{splitted}\:\mathrm{into} \\ $$$$\mathrm{2}\:\mathrm{quadratic}\:\mathrm{at}\:\mathrm{this}\:\mathrm{point}. \\ $$

Commented by ajfour last updated on 24/Jul/20

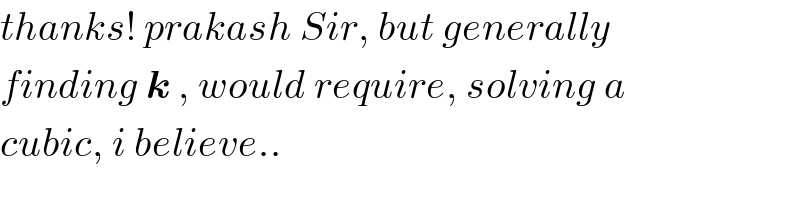
thanks! prakash Sir, but generally finding k , would require, solving a cubic, i believe..

$${thanks}!\:{prakash}\:{Sir},\:{but}\:{generally} \\ $$$${finding}\:\boldsymbol{{k}}\:,\:{would}\:{require},\:{solving}\:{a} \\ $$$${cubic},\:{i}\:{believe}.. \\ $$

Commented by prakash jain last updated on 24/Jul/20

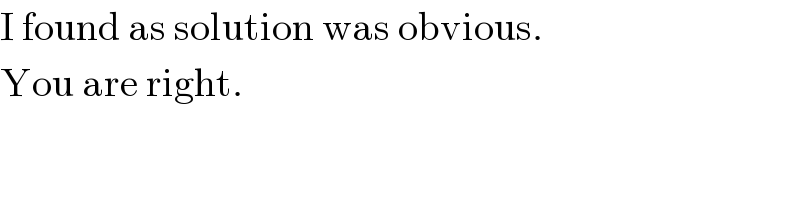
I found as solution was obvious. You are right.

$$\mathrm{I}\:\mathrm{found}\:\mathrm{as}\:\mathrm{solution}\:\mathrm{was}\:\mathrm{obvious}. \\ $$$$\mathrm{You}\:\mathrm{are}\:\mathrm{right}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply