Question Number 82891 by jagoll last updated on 25/Feb/20
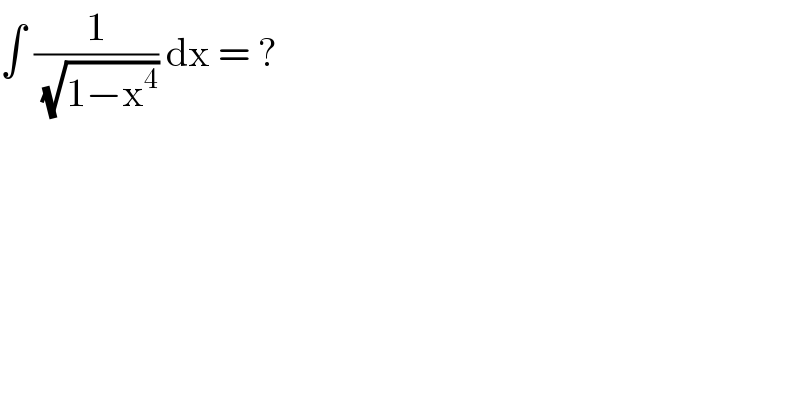
$$\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }}\:\mathrm{dx}\:=\:? \\ $$
Answered by mind is power last updated on 25/Feb/20
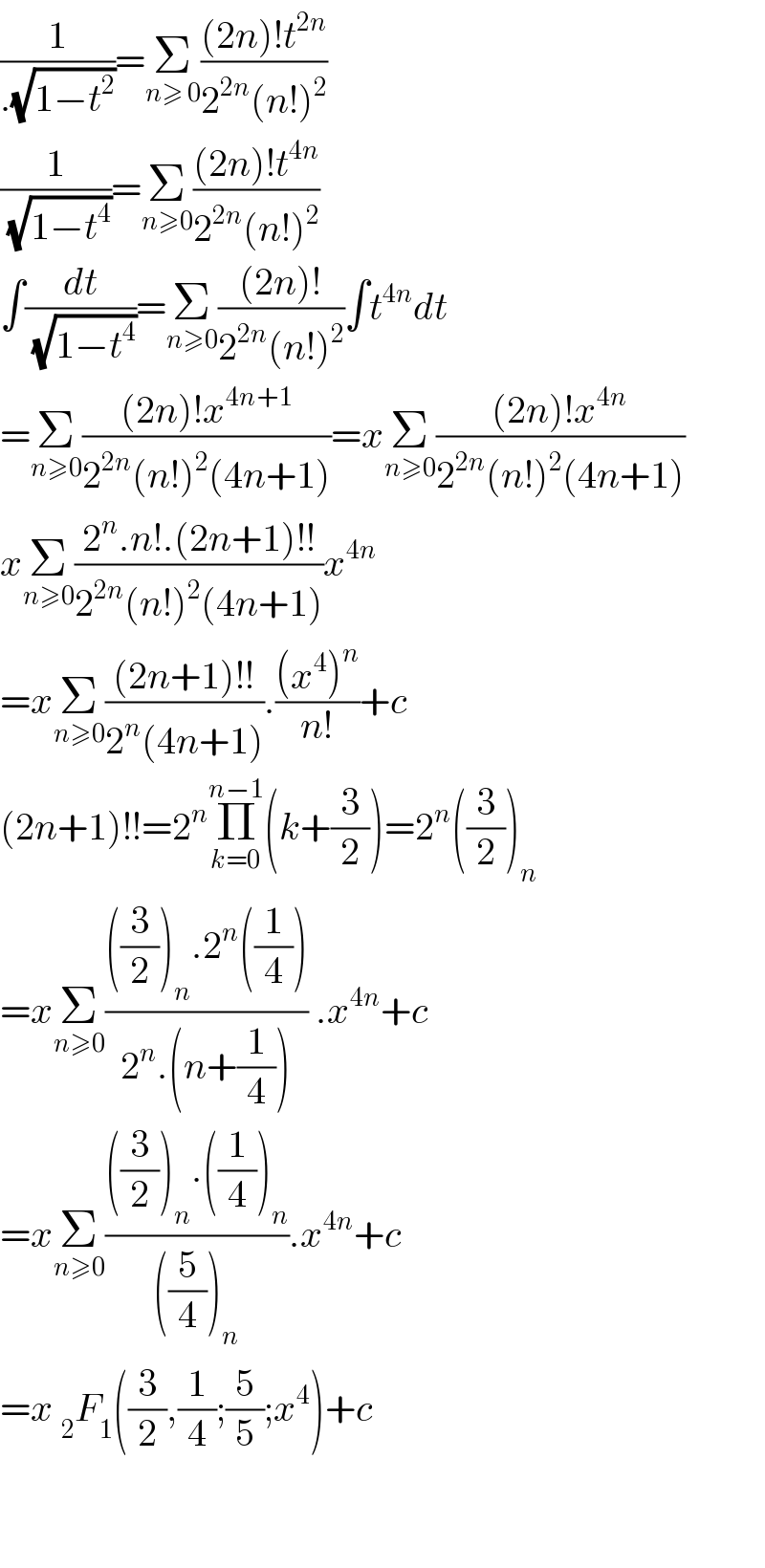
$$\frac{\mathrm{1}}{.\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\underset{{n}\geqslant\:\mathrm{0}} {\sum}\frac{\left(\mathrm{2}{n}\right)!{t}^{\mathrm{2}{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(\mathrm{2}{n}\right)!{t}^{\mathrm{4}{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} } \\ $$$$\int\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }\int{t}^{\mathrm{4}{n}} {dt} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(\mathrm{2}{n}\right)!{x}^{\mathrm{4}{n}+\mathrm{1}} }{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} \left(\mathrm{4}{n}+\mathrm{1}\right)}={x}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(\mathrm{2}{n}\right)!{x}^{\mathrm{4}{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} \left(\mathrm{4}{n}+\mathrm{1}\right)} \\ $$$${x}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{2}^{{n}} .{n}!.\left(\mathrm{2}{n}+\mathrm{1}\right)!!}{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} \left(\mathrm{4}{n}+\mathrm{1}\right)}{x}^{\mathrm{4}{n}} \\ $$$$={x}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)!!}{\mathrm{2}^{{n}} \left(\mathrm{4}{n}+\mathrm{1}\right)}.\frac{\left({x}^{\mathrm{4}} \right)^{{n}} }{{n}!}+{c} \\ $$$$\left(\mathrm{2}{n}+\mathrm{1}\right)!!=\mathrm{2}^{{n}} \underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({k}+\frac{\mathrm{3}}{\mathrm{2}}\right)=\mathrm{2}^{{n}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)_{{n}} \\ $$$$={x}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)_{{n}} .\mathrm{2}^{{n}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{2}^{{n}} .\left({n}+\frac{\mathrm{1}}{\mathrm{4}}\right)}\:.{x}^{\mathrm{4}{n}} +{c} \\ $$$$={x}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)_{{n}} .\left(\frac{\mathrm{1}}{\mathrm{4}}\right)_{{n}} }{\left(\frac{\mathrm{5}}{\mathrm{4}}\right)_{{n}} }.{x}^{\mathrm{4}{n}} +{c} \\ $$$$={x}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{4}};\frac{\mathrm{5}}{\mathrm{5}};{x}^{\mathrm{4}} \right)+{c} \\ $$$$ \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 25/Feb/20

$${great}\:{sir}\: \\ $$
Commented by jagoll last updated on 26/Feb/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by M±th+et£s last updated on 25/Feb/20
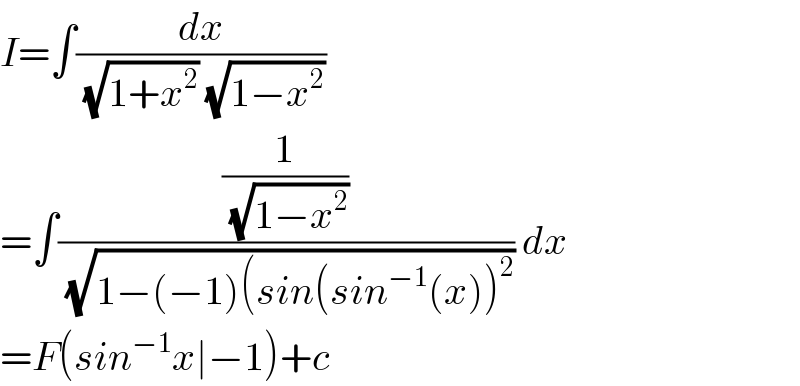
$${I}=\int\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$=\int\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{1}−\left(−\mathrm{1}\right)\left({sin}\left({sin}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} \right.}}\:{dx} \\ $$$$={F}\left({sin}^{−\mathrm{1}} {x}\mid−\mathrm{1}\right)+{c} \\ $$
Commented by M±th+et£s last updated on 25/Feb/20
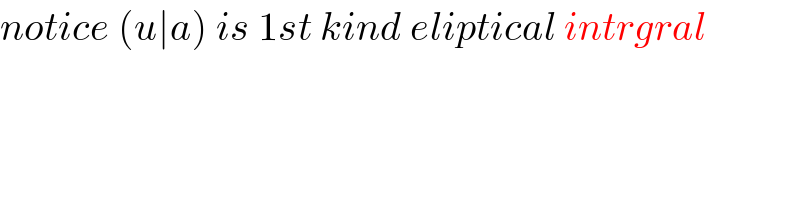
$${notice}\:\left({u}\mid{a}\right)\:{is}\:\mathrm{1}{st}\:{kind}\:{eliptical}\:{intrgral} \\ $$
