Menu Close

1-1-x-x-1-1-1-2019-2019-

Tinku Tara 0 Comments
Pin




Question Number 156107 by cortano last updated on 08/Oct/21
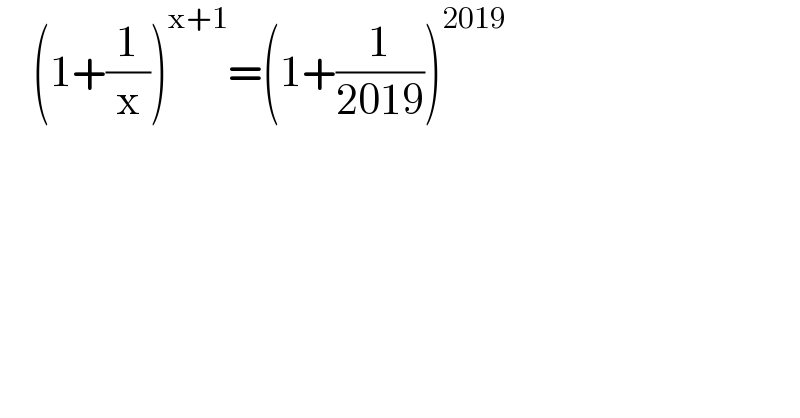
(1+(1/x))^(x+1) =(1+(1/(2019)))^(2019)
$$\:\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{x}+\mathrm{1}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2019}}\right)^{\mathrm{2019}} \\ $$
Commented by mr W last updated on 08/Oct/21
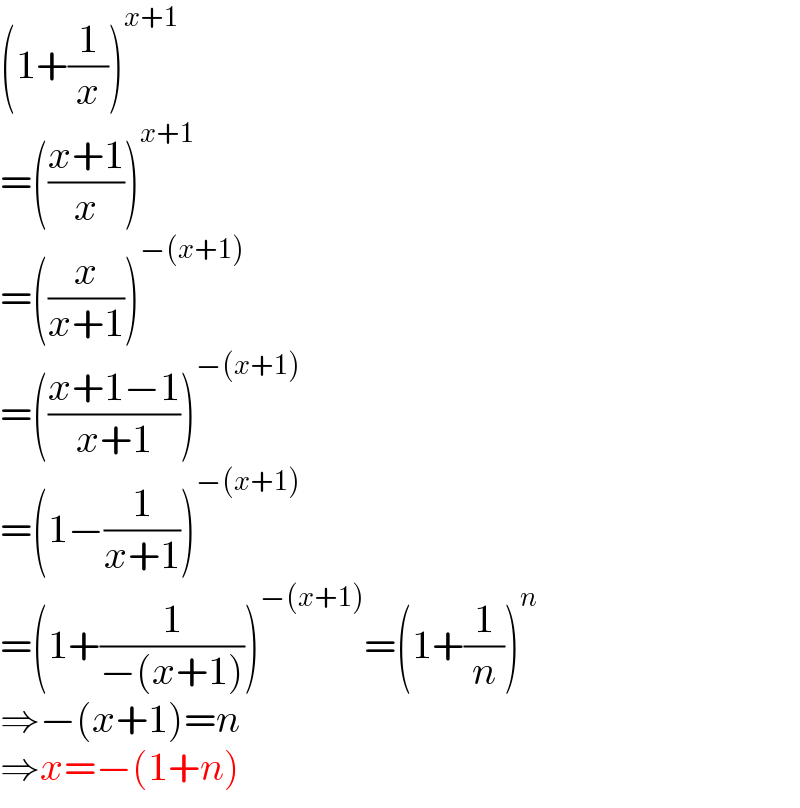
(1+(1/x))^(x+1) =(((x+1)/x))^(x+1) =((x/(x+1)))^(−(x+1)) =(((x+1−1)/(x+1)))^(−(x+1)) =(1−(1/(x+1)))^(−(x+1)) =(1+(1/(−(x+1))))^(−(x+1)) =(1+(1/n))^n ⇒−(x+1)=n ⇒x=−(1+n)
$$\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}+\mathrm{1}} \\ $$$$=\left(\frac{{x}+\mathrm{1}}{{x}}\right)^{{x}+\mathrm{1}} \\ $$$$=\left(\frac{{x}}{{x}+\mathrm{1}}\right)^{−\left({x}+\mathrm{1}\right)} \\ $$$$=\left(\frac{{x}+\mathrm{1}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{−\left({x}+\mathrm{1}\right)} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)^{−\left({x}+\mathrm{1}\right)} \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{−\left({x}+\mathrm{1}\right)}\right)^{−\left({x}+\mathrm{1}\right)} =\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \\ $$$$\Rightarrow−\left({x}+\mathrm{1}\right)={n} \\ $$$$\Rightarrow{x}=−\left(\mathrm{1}+{n}\right) \\ $$
Answered by VIDDD last updated on 08/Oct/21
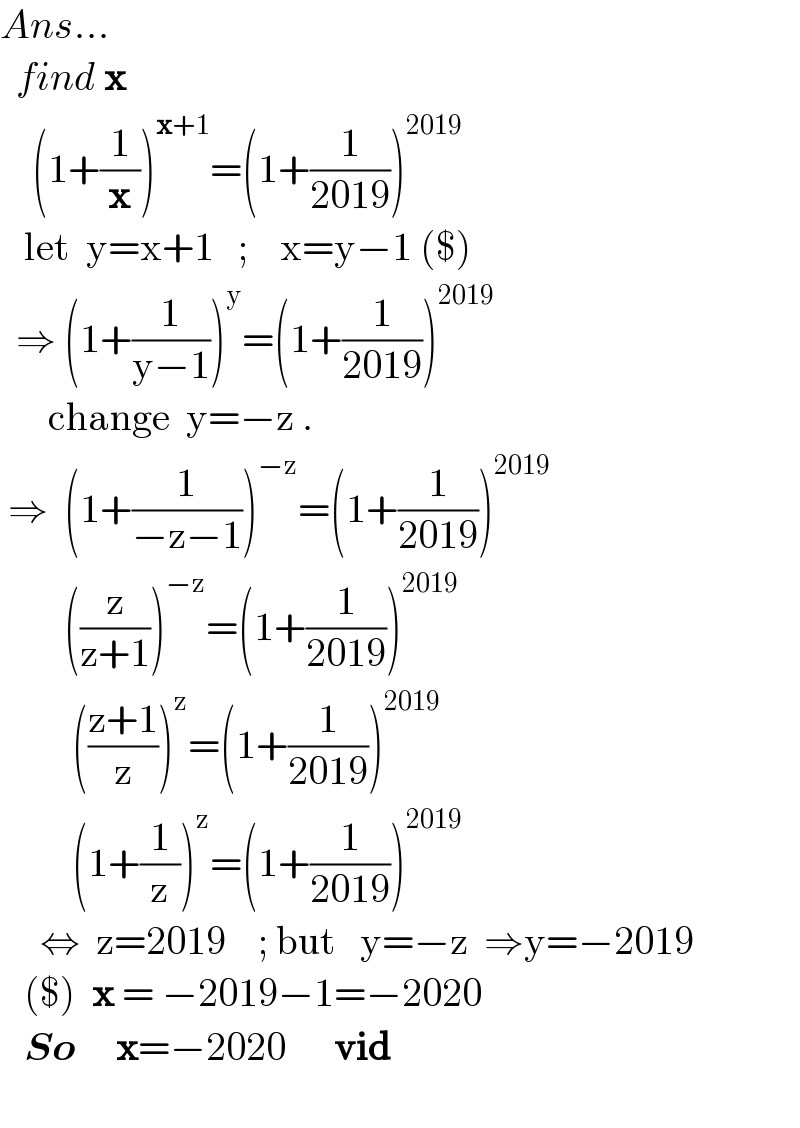
Ans... find x (1+(1/x))^(x+1) =(1+(1/(2019)))^(2019) let y=x+1 ; x=y−1 ($) ⇒ (1+(1/(y−1)))^y =(1+(1/(2019)))^(2019) change y=−z . ⇒ (1+(1/(−z−1)))^(−z) =(1+(1/(2019)))^(2019) ((z/(z+1)))^(−z) =(1+(1/(2019)))^(2019) (((z+1)/z))^z =(1+(1/(2019)))^(2019) (1+(1/z))^z =(1+(1/(2019)))^(2019) ⇔ z=2019 ; but y=−z ⇒y=−2019 ($) x = −2019−1=−2020 So x=−2020 vid
$${Ans}… \\ $$$$\:\:{find}\:\boldsymbol{\mathrm{x}} \\ $$$$\:\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)^{\boldsymbol{\mathrm{x}}+\mathrm{1}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2019}}\right)^{\mathrm{2019}} \\ $$$$\:\:\:\mathrm{let}\:\:\mathrm{y}=\mathrm{x}+\mathrm{1}\:\:\:;\:\:\:\:\mathrm{x}=\mathrm{y}−\mathrm{1}\:\left(\$\right) \\ $$$$\:\:\Rightarrow\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{y}−\mathrm{1}}\right)^{\mathrm{y}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2019}}\right)^{\mathrm{2019}} \\ $$$$\:\:\:\:\:\:\mathrm{change}\:\:\mathrm{y}=−\mathrm{z}\:. \\ $$$$\:\Rightarrow\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{−\mathrm{z}−\mathrm{1}}\right)^{−\mathrm{z}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2019}}\right)^{\mathrm{2019}} \\ $$$$\:\:\:\:\:\:\:\:\left(\frac{\mathrm{z}}{\mathrm{z}+\mathrm{1}}\right)^{−\mathrm{z}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2019}}\right)^{\mathrm{2019}} \\ $$$$\:\:\:\:\:\:\:\:\:\left(\frac{\mathrm{z}+\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{z}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2019}}\right)^{\mathrm{2019}} \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{z}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2019}}\right)^{\mathrm{2019}} \\ $$$$\:\:\:\:\:\Leftrightarrow\:\:\mathrm{z}=\mathrm{2019}\:\:\:\:;\:\mathrm{but}\:\:\:\mathrm{y}=−\mathrm{z}\:\:\Rightarrow\mathrm{y}=−\mathrm{2019} \\ $$$$\:\:\:\left(\$\right)\:\:\boldsymbol{\mathrm{x}}\:=\:−\mathrm{2019}−\mathrm{1}=−\mathrm{2020} \\ $$$$\:\:\:\boldsymbol{{So}}\:\:\:\:\:\boldsymbol{\mathrm{x}}=−\mathrm{2020}\:\:\:\:\:\:\boldsymbol{\mathrm{vid}} \\ $$$$\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *