Question Number 64410 by mmkkmm000m last updated on 17/Jul/19
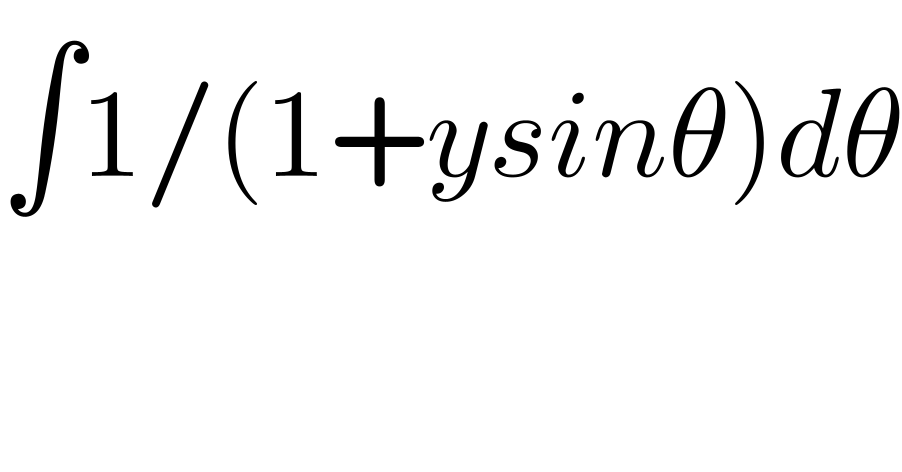
$$\int\mathrm{1}/\left(\mathrm{1}+{ysin}\theta\right){d}\theta \\ $$
Commented by mr W last updated on 17/Jul/19

$${see}\:{Q}\mathrm{64238}\:{sir}! \\ $$
Commented by Tony Lin last updated on 17/Jul/19
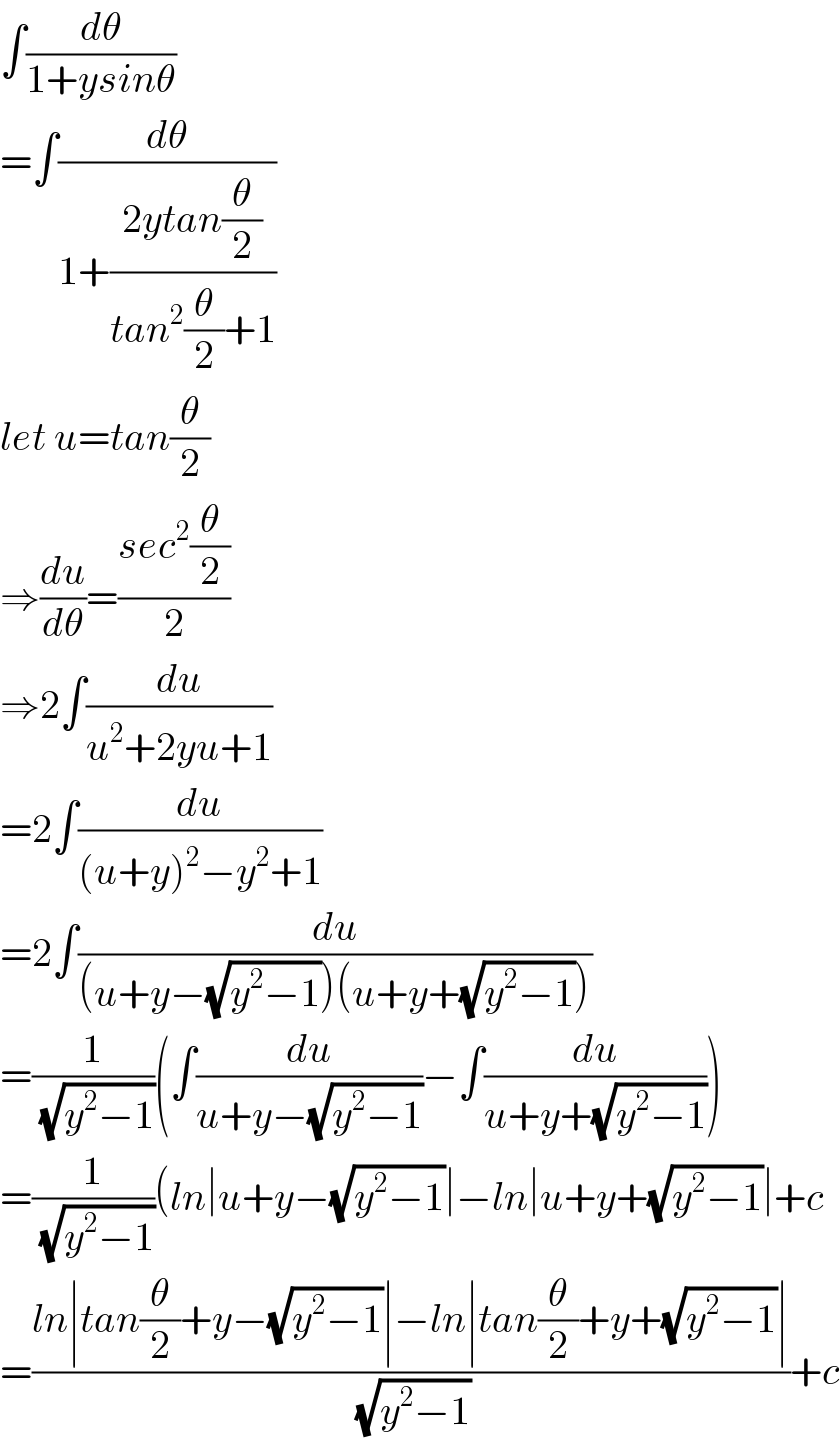
$$\int\frac{{d}\theta}{\mathrm{1}+{ysin}\theta} \\ $$$$=\int\frac{{d}\theta}{\mathrm{1}+\frac{\mathrm{2}{ytan}\frac{\theta}{\mathrm{2}}}{{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+\mathrm{1}}} \\ $$$${let}\:{u}={tan}\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{du}}{{d}\theta}=\frac{{sec}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{2}{yu}+\mathrm{1}} \\ $$$$=\mathrm{2}\int\frac{{du}}{\left({u}+{y}\right)^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\mathrm{2}\int\frac{{du}}{\left({u}+{y}−\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\right)\left({u}+{y}+\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}}\left(\int\frac{{du}}{{u}+{y}−\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}}−\int\frac{{du}}{{u}+{y}+\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}}\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}}\left({ln}\mid{u}+{y}−\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\mid−{ln}\mid{u}+{y}+\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\mid+{c}\right. \\ $$$$=\frac{{ln}\mid{tan}\frac{\theta}{\mathrm{2}}+{y}−\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\mid−{ln}\mid{tan}\frac{\theta}{\mathrm{2}}+{y}+\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\mid}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}}+{c} \\ $$
Answered by Tony Lin last updated on 17/Jul/19
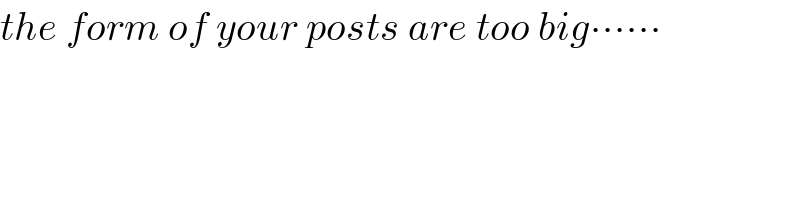
$${the}\:{form}\:{of}\:{your}\:{posts}\:{are}\:{too}\:{big}\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot \\ $$
Commented by mr W last updated on 17/Jul/19
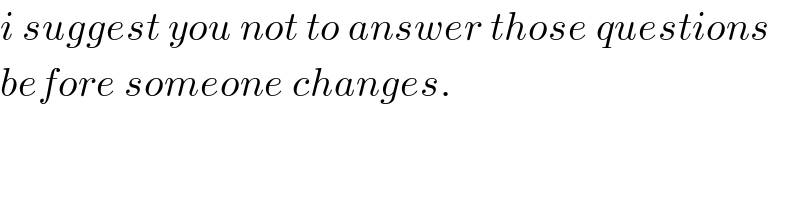
$${i}\:{suggest}\:{you}\:{not}\:{to}\:{answer}\:{those}\:{questions} \\ $$$${before}\:{someone}\:{changes}. \\ $$
