Question Number 160191 by mkam last updated on 25/Nov/21
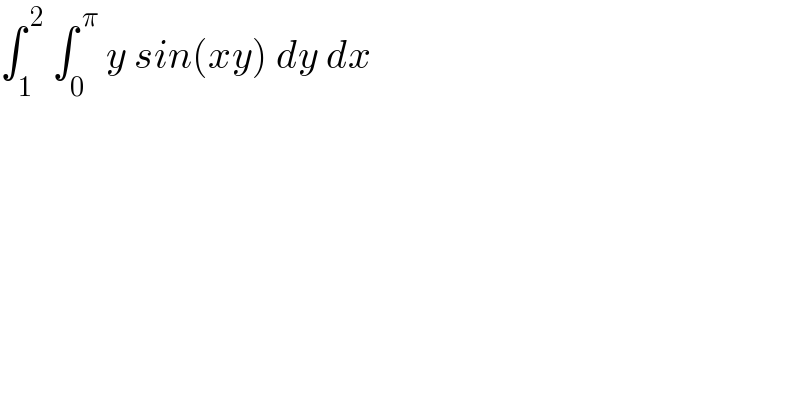
$$\int_{\mathrm{1}} ^{\:\mathrm{2}} \:\int_{\mathrm{0}} ^{\:\pi} \:{y}\:{sin}\left({xy}\right)\:{dy}\:{dx} \\ $$
Answered by mr W last updated on 25/Nov/21
![generally ∫_a ^b ∫_c ^d F(x,y)dydx=∫_c ^d ∫_a ^b F(x,y)dxdy with a,b,c,d=constants ∫_1 ^( 2) ∫_0 ^( π) y sin(xy) dy dx =∫_0 ^π ∫_1 ^( 2) y sin(yx) dx dy =∫_0 ^^π [ −cos (xy)]_1 ^2 dy =∫_0 ^^π [ cos (y)−cos (2y)] dy =[sin (y)−((sin (2y))/2)]_0 ^π =0](https://www.tinkutara.com/question/Q160199.png)
$${generally} \\ $$$$\int_{{a}} ^{{b}} \int_{{c}} ^{{d}} {F}\left({x},{y}\right){dydx}=\int_{{c}} ^{{d}} \int_{{a}} ^{{b}} {F}\left({x},{y}\right){dxdy} \\ $$$${with}\:{a},{b},{c},{d}={constants} \\ $$$$ \\ $$$$\int_{\mathrm{1}} ^{\:\mathrm{2}} \:\int_{\mathrm{0}} ^{\:\pi} \:{y}\:{sin}\left({xy}\right)\:{dy}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\int_{\mathrm{1}} ^{\:\mathrm{2}} \:{y}\:{sin}\left({yx}\right)\:{dx}\:{dy} \\ $$$$=\int_{\mathrm{0}} ^{\:^{\pi} } \left[\:−\mathrm{cos}\:\left({xy}\right)\right]_{\mathrm{1}} ^{\mathrm{2}} \:{dy} \\ $$$$=\int_{\mathrm{0}} ^{\:^{\pi} } \left[\:\mathrm{cos}\:\left({y}\right)−\mathrm{cos}\:\left(\mathrm{2}{y}\right)\right]\:{dy} \\ $$$$=\left[\mathrm{sin}\:\left({y}\right)−\frac{\mathrm{sin}\:\left(\mathrm{2}{y}\right)}{\mathrm{2}}\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\mathrm{0} \\ $$
Commented by mr W last updated on 26/Nov/21
![or (not so good way) ∫_1 ^( 2) ∫_0 ^( π) y sin(xy) dy dx =∫_1 ^( 2) {−(1/x) ∫_0 ^( π) y d[cos (xy)]}dx =∫_1 ^( 2) (1/x){−[ycos (xy)]_0 ^π +∫_0 ^( π) cos (xy)dy }dx =∫_1 ^( 2) (1/x){−[ycos (xy)]_0 ^π +[((sin (xy))/x)]_0 ^π }dx =∫_1 ^( 2) (1/x){−πcos (xπ)+((sin (xπ))/x)}dx =∫_1 ^( 2) {−((πcos (πx))/x)+((sin (πx))/x^2 )}dx =∫_1 ^( 2) d(−((sin (πx))/x)) =[−((sin (πx))/x)]_1 ^2 =((sin π)/1)−((sin 2π)/2) =0](https://www.tinkutara.com/question/Q160200.png)
$${or}\:\left({not}\:{so}\:{good}\:{way}\right) \\ $$$$\int_{\mathrm{1}} ^{\:\mathrm{2}} \:\int_{\mathrm{0}} ^{\:\pi} \:{y}\:{sin}\left({xy}\right)\:{dy}\:{dx} \\ $$$$=\int_{\mathrm{1}} ^{\:\mathrm{2}} \left\{−\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\:\pi} \:{y}\:{d}\left[\mathrm{cos}\:\left({xy}\right)\right]\right\}{dx} \\ $$$$=\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{{x}}\left\{−\left[{y}\mathrm{cos}\:\left({xy}\right)\right]_{\mathrm{0}} ^{\pi} +\int_{\mathrm{0}} ^{\:\pi} \:\mathrm{cos}\:\left({xy}\right){dy}\:\right\}{dx} \\ $$$$=\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{{x}}\left\{−\left[{y}\mathrm{cos}\:\left({xy}\right)\right]_{\mathrm{0}} ^{\pi} +\left[\frac{\mathrm{sin}\:\left({xy}\right)}{{x}}\right]_{\mathrm{0}} ^{\pi} \right\}{dx} \\ $$$$=\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{{x}}\left\{−\pi\mathrm{cos}\:\left({x}\pi\right)+\frac{\mathrm{sin}\:\left({x}\pi\right)}{{x}}\right\}{dx} \\ $$$$=\int_{\mathrm{1}} ^{\:\mathrm{2}} \left\{−\frac{\pi\mathrm{cos}\:\left(\pi{x}\right)}{{x}}+\frac{\mathrm{sin}\:\left(\pi{x}\right)}{{x}^{\mathrm{2}} }\right\}{dx} \\ $$$$=\int_{\mathrm{1}} ^{\:\mathrm{2}} {d}\left(−\frac{\mathrm{sin}\:\left(\pi{x}\right)}{{x}}\right) \\ $$$$=\left[−\frac{\mathrm{sin}\:\left(\pi{x}\right)}{{x}}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{sin}\:\pi}{\mathrm{1}}−\frac{\mathrm{sin}\:\mathrm{2}\pi}{\mathrm{2}} \\ $$$$=\mathrm{0} \\ $$
