Question Number 24831 by Eng.Firas last updated on 27/Nov/17
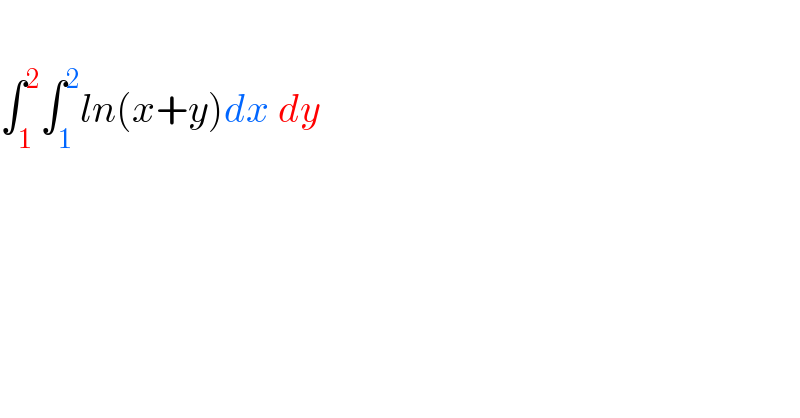
$$ \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \int_{\mathrm{1}} ^{\mathrm{2}} {ln}\left({x}+{y}\right){dx}\:{dy} \\ $$
Answered by prakash jain last updated on 27/Nov/17
![∫_1 ^2 ∫_1 ^2 ln(x+y)dxdy =∫_1 ^2 [(x+y)ln (x+y)−x]_1 ^2 dy =∫_1 ^2 {(2+y)ln (y+2)−2−(1+y)ln (1+y)+1}dy =∫_1 ^2 {(2+y)ln (y+2)−(1+y)ln (1+y)−1}dy ∫_1 ^2 (2+y)ln (y+2)dy =[ln (y+2)(((2+y)^2 )/2)−(((2+y)^2 )/4)]_1 ^2 =[(ln 4)(4^2 /2)−(4^2 /4)−(ln 3)(3^2 /2)+(3^2 /4)] =8ln 4−8−(9/2)ln 3+(9/4) ∫_1 ^2 (1+y)ln (y+1)dy =[ln (y+1)(((1+y)^2 )/2)−(((1+y)^2 )/4)]_1 ^2 =(9/2)ln 3−(9/4)−(2^2 /2)ln 2+(2^2 /4) ∫_1 ^2 (−1)dy=−1 ans=8ln 4−8−2ln 2+1−1 =16ln 2−8−2ln 2 =14ln 2−8](https://www.tinkutara.com/question/Q24850.png)
$$\int_{\mathrm{1}} ^{\mathrm{2}} \int_{\mathrm{1}} ^{\mathrm{2}} {ln}\left({x}+{y}\right){dxdy} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \left[\left({x}+{y}\right)\mathrm{ln}\:\left({x}+{y}\right)−{x}\right]_{\mathrm{1}} ^{\mathrm{2}} {dy} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \left\{\left(\mathrm{2}+{y}\right)\mathrm{ln}\:\left({y}+\mathrm{2}\right)−\mathrm{2}−\left(\mathrm{1}+{y}\right)\mathrm{ln}\:\left(\mathrm{1}+{y}\right)+\mathrm{1}\right\}\mathrm{d}{y} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \left\{\left(\mathrm{2}+{y}\right)\mathrm{ln}\:\left({y}+\mathrm{2}\right)−\left(\mathrm{1}+{y}\right)\mathrm{ln}\:\left(\mathrm{1}+{y}\right)−\mathrm{1}\right\}\mathrm{d}{y} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{2}+{y}\right)\mathrm{ln}\:\left({y}+\mathrm{2}\right){dy} \\ $$$$=\left[\mathrm{ln}\:\left({y}+\mathrm{2}\right)\frac{\left(\mathrm{2}+{y}\right)^{\mathrm{2}} }{\mathrm{2}}−\frac{\left(\mathrm{2}+{y}\right)^{\mathrm{2}} }{\mathrm{4}}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\left[\left(\mathrm{ln}\:\mathrm{4}\right)\frac{\mathrm{4}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{4}^{\mathrm{2}} }{\mathrm{4}}−\left(\mathrm{ln}\:\mathrm{3}\right)\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{4}}\right] \\ $$$$=\mathrm{8ln}\:\mathrm{4}−\mathrm{8}−\frac{\mathrm{9}}{\mathrm{2}}\mathrm{ln}\:\mathrm{3}+\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{1}+{y}\right)\mathrm{ln}\:\left({y}+\mathrm{1}\right){dy} \\ $$$$=\left[\mathrm{ln}\:\left({y}+\mathrm{1}\right)\frac{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} }{\mathrm{2}}−\frac{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} }{\mathrm{4}}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\mathrm{ln}\:\mathrm{3}−\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}\mathrm{ln}\:\mathrm{2}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \left(−\mathrm{1}\right){dy}=−\mathrm{1} \\ $$$${ans}=\mathrm{8ln}\:\mathrm{4}−\mathrm{8}−\mathrm{2ln}\:\mathrm{2}+\mathrm{1}−\mathrm{1} \\ $$$$=\mathrm{16ln}\:\mathrm{2}−\mathrm{8}−\mathrm{2ln}\:\mathrm{2} \\ $$$$=\mathrm{14ln}\:\mathrm{2}−\mathrm{8} \\ $$
Commented by Eng.Firas last updated on 27/Nov/17

$${thank}\:{you} \\ $$
