Question Number 99975 by Dwaipayan Shikari last updated on 24/Jun/20
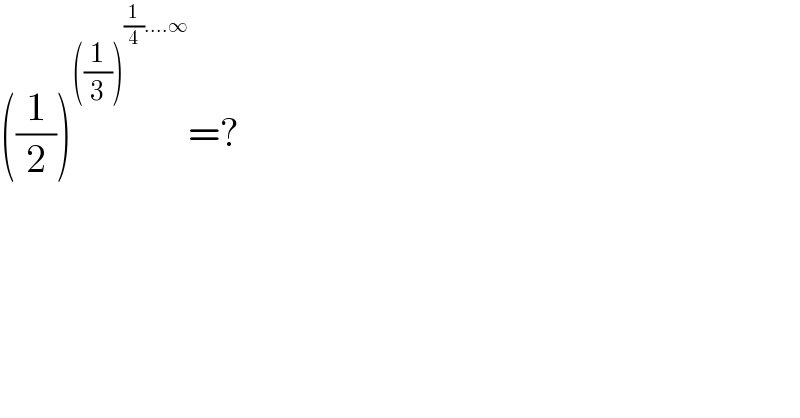
$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}….\infty} } =? \\ $$
Answered by bachamohamed last updated on 24/Jun/20
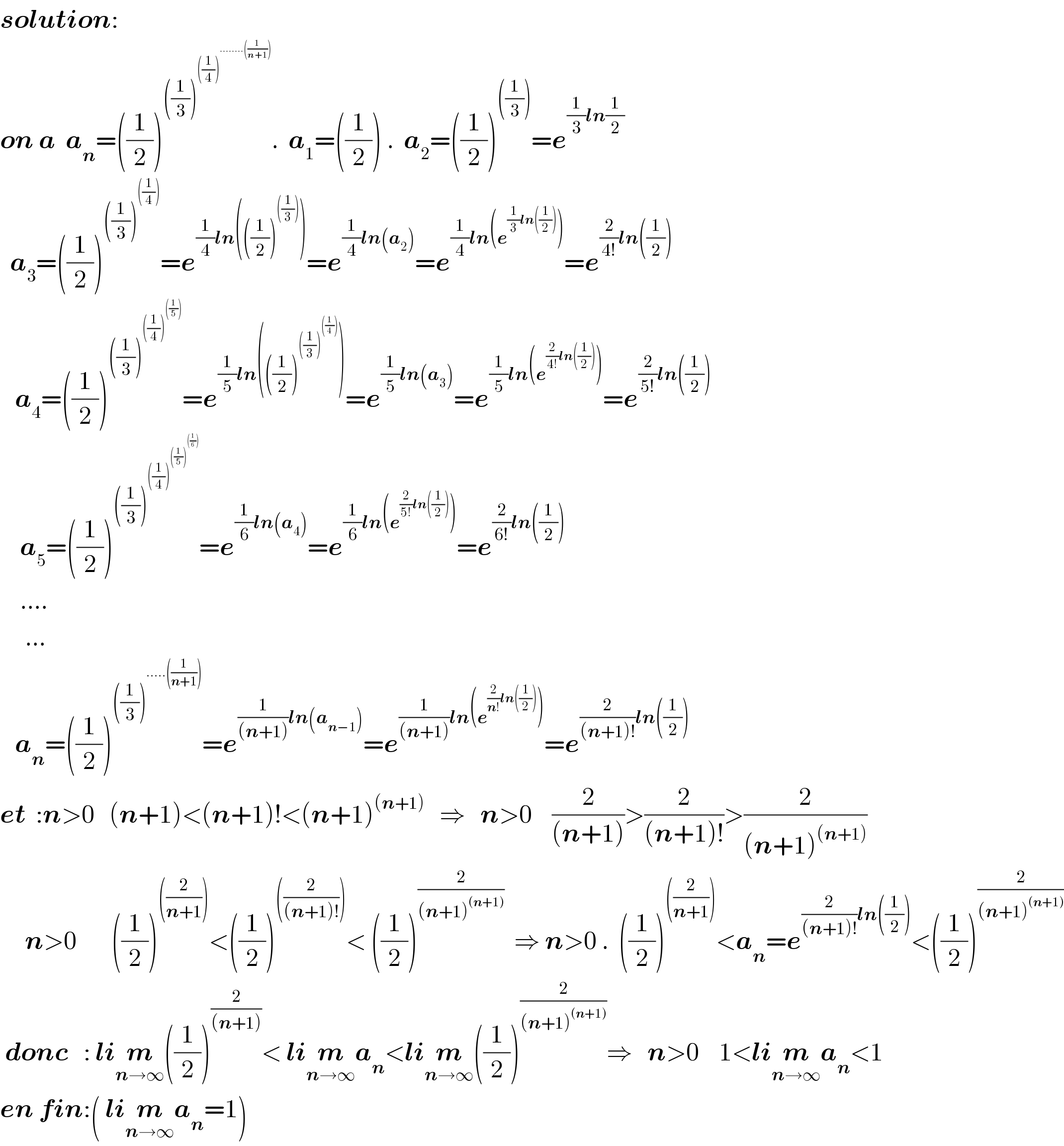
$$\boldsymbol{{solution}}:\: \\ $$$$\boldsymbol{{on}}\:\boldsymbol{{a}}\:\:\boldsymbol{{a}}_{\boldsymbol{{n}}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{……..\left(\frac{\mathrm{1}}{\boldsymbol{{n}}+\mathrm{1}}\right)} } } .\:\:\boldsymbol{{a}}_{\mathrm{1}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:.\:\:\boldsymbol{{a}}_{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{ln}}\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\boldsymbol{{a}}_{\mathrm{3}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)} } =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{ln}}\left(\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} \right)} =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{ln}}\left(\boldsymbol{{a}}_{\mathrm{2}} \right)} =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{{ln}}\left(\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \right)} =\boldsymbol{{e}}^{\frac{\mathrm{2}}{\mathrm{4}!}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\:\:\:\boldsymbol{{a}}_{\mathrm{4}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{5}}\right)} } } =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{5}}\boldsymbol{{ln}}\left(\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)} } \right)} =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{5}}\boldsymbol{{ln}}\left(\boldsymbol{{a}}_{\mathrm{3}} \right)} =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{5}}\boldsymbol{{ln}}\left(\boldsymbol{{e}}^{\frac{\mathrm{2}}{\mathrm{4}!}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \right)} =\boldsymbol{{e}}^{\frac{\mathrm{2}}{\mathrm{5}!}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:\boldsymbol{{a}}_{\mathrm{5}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)} } } } =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{{ln}}\left(\boldsymbol{{a}}_{\mathrm{4}} \right)} =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{{ln}}\left(\boldsymbol{{e}}^{\frac{\mathrm{2}}{\mathrm{5}!}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \right)} =\boldsymbol{{e}}^{\frac{\mathrm{2}}{\mathrm{6}!}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:…. \\ $$$$\:\:\:\:\:… \\ $$$$\:\:\:\boldsymbol{{a}}_{\boldsymbol{{n}}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{…..\left(\frac{\mathrm{1}}{\boldsymbol{{n}}+\mathrm{1}}\right)} } =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)}\boldsymbol{{ln}}\left(\boldsymbol{{a}}_{\boldsymbol{{n}}−\mathrm{1}} \right)} =\boldsymbol{{e}}^{\frac{\mathrm{1}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)}\boldsymbol{{ln}}\left(\boldsymbol{{e}}^{\frac{\mathrm{2}}{\boldsymbol{{n}}!}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \right)} =\boldsymbol{{e}}^{\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)!}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\boldsymbol{{et}}\:\::\boldsymbol{{n}}>\mathrm{0}\:\:\:\left(\boldsymbol{{n}}+\mathrm{1}\right)<\left(\boldsymbol{{n}}+\mathrm{1}\right)!<\left(\boldsymbol{{n}}+\mathrm{1}\right)^{\left(\boldsymbol{{n}}+\mathrm{1}\right)} \:\:\:\Rightarrow\:\:\:\boldsymbol{{n}}>\mathrm{0}\:\:\:\:\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)}>\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)!}>\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)^{\left(\boldsymbol{{n}}+\mathrm{1}\right)} }\: \\ $$$$\:\:\:\:\:\boldsymbol{{n}}>\mathrm{0}\:\:\:\:\:\:\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{2}}{\boldsymbol{{n}}+\mathrm{1}}\right)} <\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)!}\right)} <\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)^{\left(\boldsymbol{{n}}+\mathrm{1}\right)} }} \:\:\Rightarrow\:\boldsymbol{{n}}>\mathrm{0}\:.\:\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{2}}{\boldsymbol{{n}}+\mathrm{1}}\right)} <\boldsymbol{{a}}_{\boldsymbol{{n}}} =\boldsymbol{{e}}^{\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)!}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} <\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)^{\left(\boldsymbol{{n}}+\mathrm{1}\right)} }} \\ $$$$\:\boldsymbol{{donc}}\:\:\::\:\boldsymbol{{li}}\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{m}}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)}} <\:\boldsymbol{{li}}\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{m}a}}_{\boldsymbol{{n}}} <\boldsymbol{{li}}\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{m}}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)^{\left(\boldsymbol{{n}}+\mathrm{1}\right)} }} \Rightarrow\:\:\:\boldsymbol{{n}}>\mathrm{0}\:\:\:\:\mathrm{1}<\boldsymbol{{li}}\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{m}a}}_{\boldsymbol{{n}}} <\mathrm{1} \\ $$$$\boldsymbol{{en}}\:\boldsymbol{{fin}}:\left(\:\boldsymbol{{li}}\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{m}a}}_{\boldsymbol{{n}}} =\mathrm{1}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 24/Jun/20
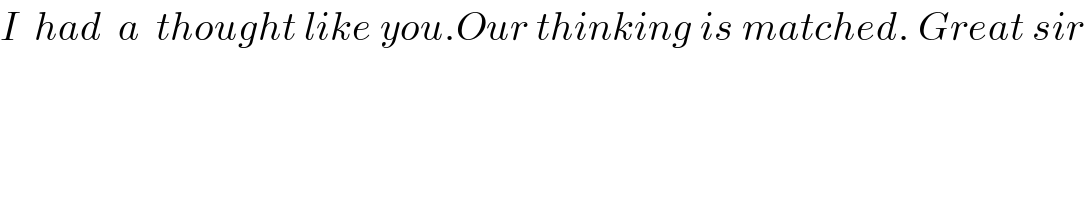
$${I}\:\:{had}\:\:{a}\:\:{thought}\:{like}\:{you}.{Our}\:{thinking}\:{is}\:{matched}.\:{Great}\:{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 24/Jun/20

$$\mathrm{Just}\:\mathrm{matched}!!\mathrm{But}\:\mathrm{i}\:\mathrm{was}\:\mathrm{not}\:\mathrm{so}\:\mathrm{sure}\:\mathrm{about}\:\mathrm{answer}.\:\mathrm{Sir}\:\mathrm{you}\:\mathrm{create}\:\mathrm{my}\:\mathrm{belief} \\ $$
Commented by bachamohamed last updated on 24/Jun/20

$$\:{thank}'\mathrm{s} \\ $$
