Question Number 129014 by bramlexs22 last updated on 12/Jan/21
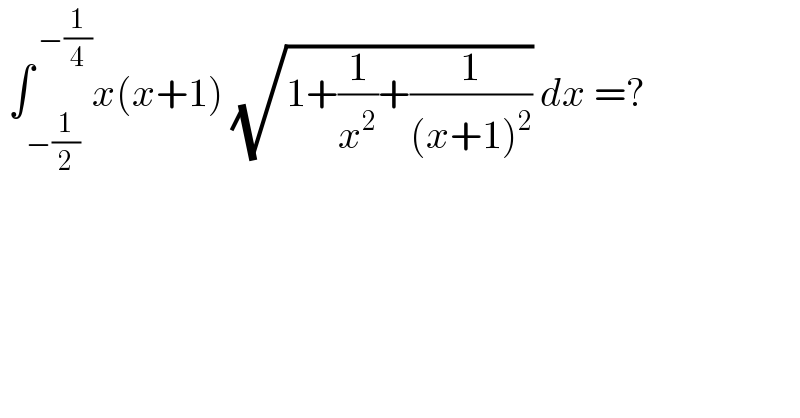
$$\:\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\:−\frac{\mathrm{1}}{\mathrm{4}}} {x}\left({x}+\mathrm{1}\right)\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }}\:{dx}\:=?\: \\ $$
Commented by Ajao yinka last updated on 12/Jan/21
37/192
Answered by liberty last updated on 12/Jan/21
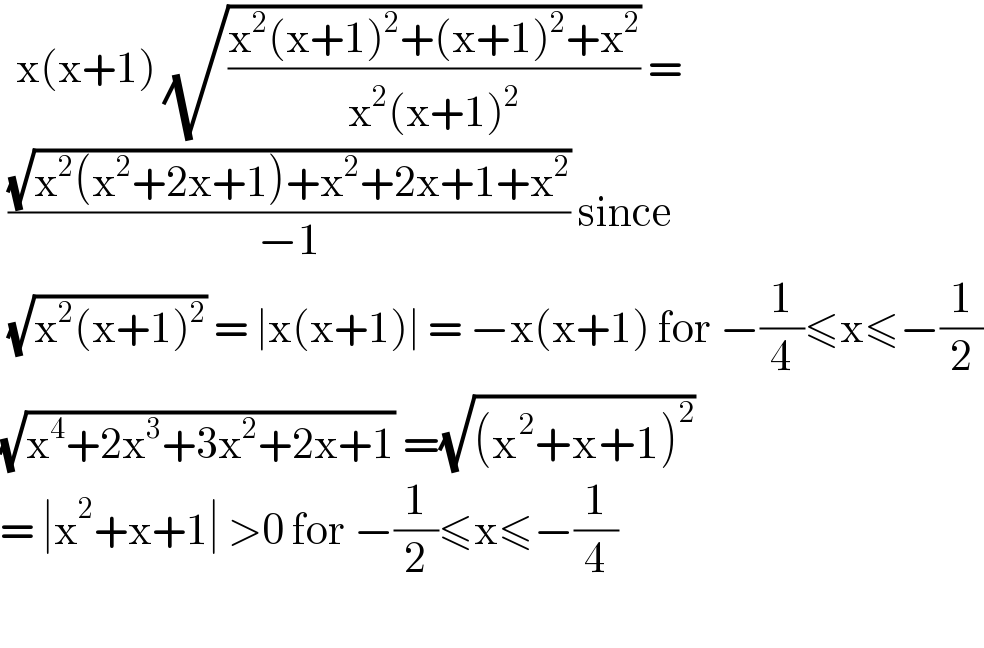
$$\:\:\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\:\sqrt{\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }}\:=\: \\ $$$$\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}\right)+\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{−\mathrm{1}}\:\mathrm{since}\: \\ $$$$\:\sqrt{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\mid\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\mid\:=\:−\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\:\mathrm{for}\:−\frac{\mathrm{1}}{\mathrm{4}}\leqslant\mathrm{x}\leqslant−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}}\:=\sqrt{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\:\mid\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\mid\:>\mathrm{0}\:\mathrm{for}\:−\frac{\mathrm{1}}{\mathrm{2}}\leqslant\mathrm{x}\leqslant−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 12/Jan/21
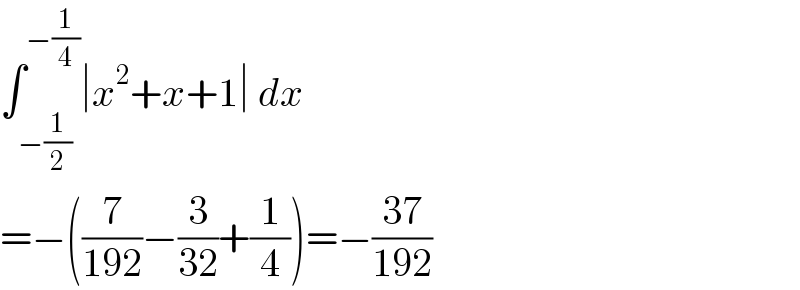
$$\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{−\frac{\mathrm{1}}{\mathrm{4}}} \mid{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid\:{dx} \\ $$$$=−\left(\frac{\mathrm{7}}{\mathrm{192}}−\frac{\mathrm{3}}{\mathrm{32}}+\frac{\mathrm{1}}{\mathrm{4}}\right)=−\frac{\mathrm{37}}{\mathrm{192}} \\ $$
