Question Number 186196 by normans last updated on 02/Feb/23
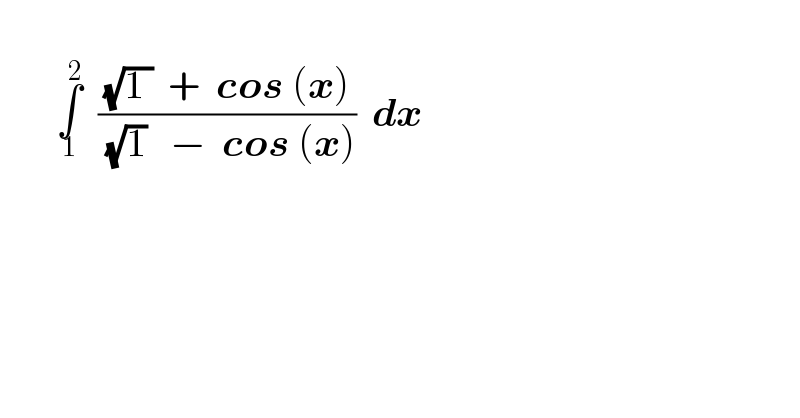
$$ \\ $$$$\:\:\:\:\:\:\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\:\frac{\sqrt{\mathrm{1}\:}\:\:+\:\:\boldsymbol{{cos}}\:\left(\boldsymbol{{x}}\right)}{\:\sqrt{\mathrm{1}}\:\:\:−\:\:\boldsymbol{{cos}}\:\left(\boldsymbol{{x}}\right)}\:\:\boldsymbol{{dx}}\:\:\:\:\:\: \\ $$$$ \\ $$
Commented by MJS_new last updated on 02/Feb/23

$$\sqrt{\mathrm{1}}\:\mathrm{are}\:\mathrm{you}\:\mathrm{sure}? \\ $$
Commented by normans last updated on 02/Feb/23

$${yes} \\ $$
Answered by CElcedricjunior last updated on 02/Feb/23
![∫_1 ^2 ((1+cosx)/(1−cosx))dx=−1+2∫_1 ^2 (1/(1−cosx))dx =−1+2∫_(1 ) ^2 (1/(2sin^2 ((x/2))))dx ] =−1+[4tan((x/2))+k]_1 ^2 ∫_1 ^2 (((√1)+cosx)/( (√1)−cosx))dx=−1+tan(1)−tan((1/2)) =======================.== ..............le celebre cedric junior.........(√)](https://www.tinkutara.com/question/Q186226.png)
$$\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}+\boldsymbol{{cosx}}}{\mathrm{1}−\boldsymbol{{cosx}}}\boldsymbol{{dx}}=−\mathrm{1}+\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{1}−\boldsymbol{{cosx}}}\boldsymbol{{dx}} \\ $$$$\:\:\:\:\:\:\:\:=−\mathrm{1}+\mathrm{2}\int_{\mathrm{1}\:} ^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{si}}\overset{\mathrm{2}} {\boldsymbol{{n}}}\left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)}\boldsymbol{{dx}} \\ $$$$\left.\:\:\:\right]\:\:\:\:=−\mathrm{1}+\left[\mathrm{4}\boldsymbol{{tan}}\left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)+\boldsymbol{{k}}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\sqrt{\mathrm{1}}+\boldsymbol{{cosx}}}{\:\sqrt{\mathrm{1}}−\boldsymbol{{cosx}}}\boldsymbol{{dx}}=−\mathrm{1}+\boldsymbol{{tan}}\left(\mathrm{1}\right)−\boldsymbol{{tan}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=======================.== \\ $$$$…………..{le}\:{celebre}\:{cedric}\:{junior}………\sqrt{} \\ $$
Answered by Mathspace last updated on 02/Feb/23
![I=∫_1 ^2 ((1+cosx)/(1−cosx))dx=∫_1 ^2 ((2cos^2 ((x/2)))/(2sin^2 ((x/2))))dx =∫_1 ^2 (((cos((x/2)))/(sin((x/2)))))^2 dx =_((x/2)=t) 2∫_(1/2) ^1 ((cos^2 t)/(sin^2 t))dt =2∫_(1/2) ^1 ((1−sin^2 t)/(sin^2 t))dt =2∫_(1/2) ^1 (dt/(sin^2 t))−1 =2∫_(1/2) ^1 (dt/((1−cos(2t))/2))−1 =4∫_(1/2) ^1 (dt/(1−cos(2t))) (2t=x)−1 =2∫_1 ^2 (dx/(1−cosx))(tan((x/2))=z)−1 =2∫_(tan((1/2))) ^(tan(1)) ((2dz)/((1+z^2 )(1−((1−z^2 )/(1+z^2 )))))−1 =4∫_(tan((1/2))) ^(tan(1)) (dz/(1+z^2 −1+z^2 ))−1 =2∫_(tan((1/2))) ^(tan(1)) (dz/z^2 )−1=2[−(1/z)]_(tan((1/2))) ^(tan(1)) −1 =2{(1/(tan((1/2))))−(1/(tan(1)))}−1](https://www.tinkutara.com/question/Q186228.png)
$${I}=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}+{cosx}}{\mathrm{1}−{cosx}}{dx}=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \left(\frac{{cos}\left(\frac{{x}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}\right)^{\mathrm{2}} {dx} \\ $$$$=_{\frac{{x}}{\mathrm{2}}={t}} \:\: \\ $$$$\mathrm{2}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{{cos}^{\mathrm{2}} {t}}{{sin}^{\mathrm{2}} {t}}{dt} \\ $$$$=\mathrm{2}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{\mathrm{1}−{sin}^{\mathrm{2}} {t}}{{sin}^{\mathrm{2}} {t}}{dt} \\ $$$$=\mathrm{2}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{{dt}}{{sin}^{\mathrm{2}} {t}}−\mathrm{1} \\ $$$$=\mathrm{2}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{{dt}}{\frac{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}−\mathrm{1} \\ $$$$=\mathrm{4}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}\:\left(\mathrm{2}{t}={x}\right)−\mathrm{1} \\ $$$$=\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{dx}}{\mathrm{1}−{cosx}}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)={z}\right)−\mathrm{1} \\ $$$$=\mathrm{2}\int_{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{{tan}\left(\mathrm{1}\right)} \frac{\mathrm{2}{dz}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{1}−{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} }\right)}−\mathrm{1} \\ $$$$=\mathrm{4}\int_{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{{tan}\left(\mathrm{1}\right)} \:\frac{{dz}}{\mathrm{1}+{z}^{\mathrm{2}} −\mathrm{1}+{z}^{\mathrm{2}} }−\mathrm{1} \\ $$$$=\mathrm{2}\int_{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{{tan}\left(\mathrm{1}\right)} \frac{{dz}}{{z}^{\mathrm{2}} }−\mathrm{1}=\mathrm{2}\left[−\frac{\mathrm{1}}{{z}}\right]_{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{{tan}\left(\mathrm{1}\right)} −\mathrm{1} \\ $$$$=\mathrm{2}\left\{\frac{\mathrm{1}}{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}−\frac{\mathrm{1}}{{tan}\left(\mathrm{1}\right)}\right\}−\mathrm{1} \\ $$
Answered by MJS_new last updated on 02/Feb/23
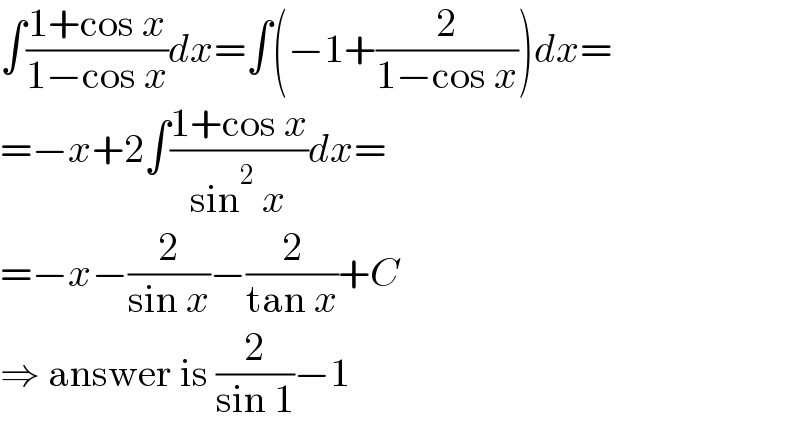
$$\int\frac{\mathrm{1}+\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{cos}\:{x}}{dx}=\int\left(−\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}−\mathrm{cos}\:{x}}\right){dx}= \\ $$$$=−{x}+\mathrm{2}\int\frac{\mathrm{1}+\mathrm{cos}\:{x}}{\mathrm{sin}^{\mathrm{2}} \:{x}}{dx}= \\ $$$$=−{x}−\frac{\mathrm{2}}{\mathrm{sin}\:{x}}−\frac{\mathrm{2}}{\mathrm{tan}\:{x}}+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{1}}−\mathrm{1} \\ $$
